题目内容
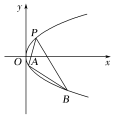
【题目】点![]() 为圆
为圆![]() 上一动点,
上一动点,![]() 轴于
轴于![]() 点,记线段
点,记线段![]() 的中点
的中点![]() 的运动轨迹为曲线
的运动轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)直线![]() 经过定点
经过定点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)1
;(2)1
【解析】
(1)利用![]() 表示出
表示出![]() ,代入圆
,代入圆![]() 方程即可得到曲线
方程即可得到曲线![]() 方程;
方程;
(2)设直线![]() 方程为
方程为![]() ,代入椭圆方程得到韦达定理形式,利用弦长公式求得
,代入椭圆方程得到韦达定理形式,利用弦长公式求得![]() ,利用点到直线距离公式求得原点到直线
,利用点到直线距离公式求得原点到直线![]() 的距离,由
的距离,由![]() 可将所求面积表示为关于斜率
可将所求面积表示为关于斜率![]() 的函数的形式,结合基本不等式求得函数的最小值,即为所求面积的最小值.
的函数的形式,结合基本不等式求得函数的最小值,即为所求面积的最小值.
(1)设![]() ,
,![]() ,
,
![]() 为圆
为圆![]() 上一动点,
上一动点,![]() 轴于
轴于![]() 点,
点,![]() 为
为![]() 的中点,
的中点,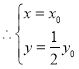 ,
,
则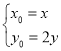 ,代入
,代入![]() 得曲线
得曲线![]() 的方程为:
的方程为:![]() .
.
(2)由题意知:直线![]() 斜率存在,可设直线
斜率存在,可设直线![]() 方程为:
方程为:![]() ,
,
设![]() ,
,![]() ,
,
由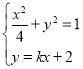 消去
消去![]() 得:
得:![]() ,
,
由![]() 得:
得:![]() 或
或![]() ,
,
![]() ,
,![]() ,
,
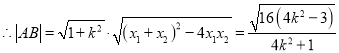 ,
,
而原点到直线![]() 的距离为
的距离为![]() ,
,
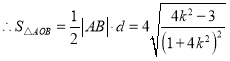
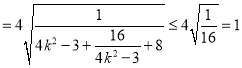 ,(当且仅当
,(当且仅当![]() ,即
,即![]() 时取等号),
时取等号),
![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:
(单位:![]() )的影响,对近
)的影响,对近![]() 年的年宣传费
年的年宣传费![]() 和年销售量
和年销售量![]() 作了初步统计和处理,得到的数据如下:
作了初步统计和处理,得到的数据如下:
年宣传费 |
|
|
|
|
年销售量 |
|
|
|
|
![]() ,
,![]() .
.

(1)在给定的坐标系中画出表中数据的散点图;
(2)求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若公司计划下一年度投入宣传费![]() 万元,试预测年销售量
万元,试预测年销售量![]() 的值.
的值.
参考公式