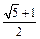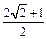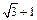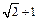题目内容
如图,椭圆中心在坐标原点,F为左焦点,当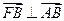 时,其离心率为
时,其离心率为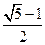 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲
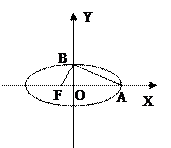
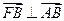 时,其离心率为
时,其离心率为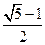 ,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲
,此类椭圆被称为“黄金椭圆”.类比“黄金椭圆”,可推算出”黄金双曲线”的离心率e等于 ▲ 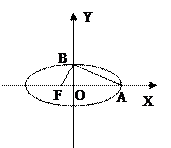
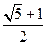
猜想出“黄金双曲线”的离心率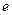 等于
等于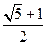 .事实上对直角△
.事实上对直角△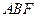 应用勾股定理,得
应用勾股定理,得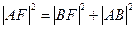 ,即有
,即有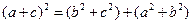 ,
,
注意到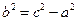 ,
, ,变形得
,变形得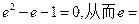
点评:本题通过圆锥曲线的有关知识考查类比推理,属于难题
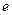 等于
等于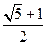 .事实上对直角△
.事实上对直角△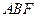 应用勾股定理,得
应用勾股定理,得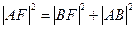 ,即有
,即有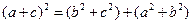 ,
,注意到
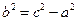 ,
, ,变形得
,变形得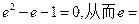
点评:本题通过圆锥曲线的有关知识考查类比推理,属于难题

练习册系列答案
相关题目
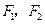 分别是双曲线
分别是双曲线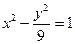 的左、右焦点.若点
的左、右焦点.若点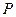 在双曲线上,且
在双曲线上,且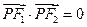 ,则
,则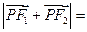 .
.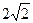 ,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.
,其焦点F(c,0)(c>0)对应的准线l与x轴交于A点,|OF|=2|FA|,过A的直线与椭圆交于P、Q两点.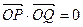 ,求直线PQ的方程; (3)设
,求直线PQ的方程; (3)设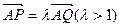 ,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.
,过点P且平行于准线l的直线与椭圆相交于另一点M. 求证F、M、Q三点共线.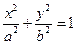 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.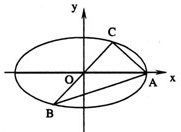
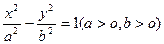 的左焦点F作倾斜角为
的左焦点F作倾斜角为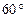 的直线与双曲线相交于A、B两点,若
的直线与双曲线相交于A、B两点,若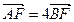 ,则双曲线的离心率为( )
,则双曲线的离心率为( )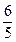 B、
B、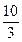 C、
C、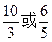 D、2
D、2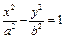 有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )
有相同焦点F,点A是两曲线交点,且AF⊥x轴,则双曲线的离心率为 ( )