题目内容
如图,已知圆G:x2+y2-2x-
y=0,经过椭圆
+
=1(a>b>0)的右焦点F及上顶点B,过圆外一点(m,0)(m>a)倾斜角为
的直线l交椭圆于C,D两点,
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.

| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 5π |
| 6 |
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.

(1)x2+y2-2x-
y=0过点F、B,
∴F(2,0),B(0,
),
故椭圆的方程为
+
=1
(2)直线l:y=-
(x-m)(m>
)
消y得2x2-2mx+(m2-6)=0
由△>0⇒-2
<m<2
,
又m>
⇒
<m<2
设C(x1,y1)、D(x2,y2),则x1+x2=m,x1x2=
,y1y2=
x1x2-
(x1+x2)+
,
=(x1-2,y1),
=(x2-2,y2)
∴
•
=(x1-2)(x2-2)+y1y2=
∵F在圆E的内部,∴
•
<0⇒0<m<3,
又
<m<2
⇒
<m<3.
| 2 |
∴F(2,0),B(0,
| 2 |
故椭圆的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(2)直线l:y=-
| ||
| 3 |
| 6 |
|
消y得2x2-2mx+(m2-6)=0
由△>0⇒-2
| 3 |
| 3 |
又m>
| 6 |
| 6 |
| 3 |
设C(x1,y1)、D(x2,y2),则x1+x2=m,x1x2=
| m2-6 |
| 2 |
| 1 |
| 3 |
| m |
| 3 |
| m2 |
| 3 |
| FC |
| FD |
∴
| FC |
| FD |
| 2m(m-3) |
| 3 |
∵F在圆E的内部,∴
| FC |
| FD |
又
| 6 |
| 3 |
| 6 |

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
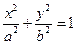 (a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.
(a>b>0)的左右顶点,P为直线x=u上不同于(u,0)的任一点,若直线AP、BP分别与椭圆交于异于A、B的点M、N,研究点B与以MN为直径的圆的位置关系.