��Ŀ����
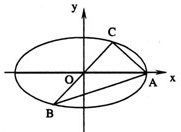
��ͼ����ƽ��ֱ������ϵxOy�У���ԲE��
+
=1(a��b��0)�Ľ���Ϊ2���ҹ���(
��
)��
��1������ԲE�ķ��̣�
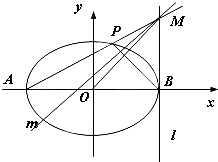
��2������A��B�ֱ�����ԲE�����Ҷ��㣬ֱ��l������B�Ҵ�ֱ��x�ᣬ��P����Բ������A��B������һ�㣬ֱ��AP��l�ڵ�M��
��������ֱ��OM��б��Ϊk1��ֱ��BP��б��Ϊk2����֤��k1k2Ϊ��ֵ��
�����������M��ֱ��PB��ֱ��Ϊm����֤��ֱ��m�����㣬�������������꣮
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
��1������ԲE�ķ��̣�
��2������A��B�ֱ�����ԲE�����Ҷ��㣬ֱ��l������B�Ҵ�ֱ��x�ᣬ��P����Բ������A��B������һ�㣬ֱ��AP��l�ڵ�M��
��������ֱ��OM��б��Ϊk1��ֱ��BP��б��Ϊk2����֤��k1k2Ϊ��ֵ��
�����������M��ֱ��PB��ֱ��Ϊm����֤��ֱ��m�����㣬�������������꣮

��1���������2c=2����c=1����
+
=1��a2=b2+1��
��ȥa�ɵã�2b4-5b2-3=0�����b2=3��b2=-
����ȥ������a2=4��
����ԲE�ķ���Ϊ
+
=1��
��2����������P��x1��y1����y1��0����M��2��y0������k1=
��k2=
��
��A��P��M���㹲�ߣ���y0=
����k1k2=
=
��
��P��x1��y1������Բ�ϣ���
=
(4-
)����k1k2=
=-
Ϊ��ֵ��
������ֱ��BP��б��Ϊk2=
��ֱ��m��б��Ϊkm=
��
��ֱ��m�ķ���Ϊy-y0=
(x-2)��y=
(x-2)+y0=
x-
+
=
x+
=
x+
=
x+
=
(x+1)��
��y=
(x+1)��
����ֱ��m�����㣨-1��0����
| 2 |
| a2 |
| 3 |
| 2b2 |
��ȥa�ɵã�2b4-5b2-3=0�����b2=3��b2=-
| 1 |
| 2 |
����ԲE�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2����������P��x1��y1����y1��0����M��2��y0������k1=
| y0 |
| 2 |
| y1 |
| x1-2 |
��A��P��M���㹲�ߣ���y0=
| 4y1 |
| x1+2 |
| y0y1 |
| 2(x1-2) |
| 4y12 | ||
2(
|
��P��x1��y1������Բ�ϣ���
| y | 21 |
| 3 |
| 4 |
| x | 21 |
| 4y12 | ||
2(
|
| 3 |
| 2 |
������ֱ��BP��б��Ϊk2=
| y1 |
| x1-2 |
| 2-x1 |
| y1 |
��ֱ��m�ķ���Ϊy-y0=
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2(2-x1) |
| y1 |
| 4y1 |
| x1+2 |
| 2-x1 |
| y1 |
2(x12-4)+4
| ||
| (x1+2)y1 |
| 2-x1 |
| y1 |
2(x12-4)+12-3
| ||
| (x1+2)y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
| 2-x1 |
| y1 |
��y=
| 2-x1 |
| y1 |
����ֱ��m�����㣨-1��0����

��ϰ��ϵ�д�
�����Ŀ
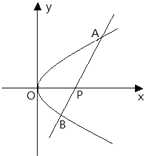
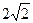 ���佹��F��c��0����c��0����Ӧ����l��x�ύ��A�㣬|OF|=2|FA|����A��ֱ������Բ����P��Q����.
���佹��F��c��0����c��0����Ӧ����l��x�ύ��A�㣬|OF|=2|FA|����A��ֱ������Բ����P��Q����.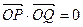 ����ֱ��PQ�ķ��̣� ��3����
����ֱ��PQ�ķ��̣� ��3����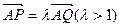 ������P��ƽ������l��ֱ������Բ�ཻ����һ��M. ��֤F��M��Q���㹲��.
������P��ƽ������l��ֱ������Բ�ཻ����һ��M. ��֤F��M��Q���㹲��.