Question

已知点P（-1，

3

2

）是椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）上一点，F₁、F₂分别是椭圆C的左、右焦点，O是坐标原点，PF₁⊥x轴．
①求椭圆C的方程；
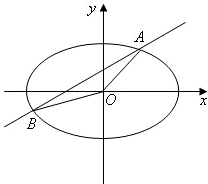
②设A、B是椭圆C上两个动点，满足

PA

+

PB

=λ

PO

（0＜λ＜4，且λ≠2）求直线AB的斜率．

Answer 1

①∵PF₁⊥x轴，∴c=1，把点P（-1，

3

2

）代入椭圆的方程得

1

a2

+

9

4b2

=1，又a²-b²=c²=1，联立解得a²=4，b²=3．
∴椭圆C的方程为

x2

4

+

y2

3

=1；
②设直线y=kx+m，联立

y=kx+m x2 4 + y2 3 =1

，化为（3+4k²）x²+8kmx+4m²-12=0，
∵直线AB与椭圆有两个不同的交点，∴△=64k²m²-4（3+4k²）（4m²-12）＞0，化为3+4k²-m²＞0．（*）
∴x1+x2=-

8km

3+4k2

．
∵满足

PA

+

PB

=λ

PO

（0＜λ＜4，且λ≠2），
∴(x1+1，y1-

3

2

)+(x2+1，y2-

3

2

)=λ(1，-

3

2

)，
∴x₁+x₂+2=λ，y1+y2-3=-

3

2

λ，
又y₁+y₂=kx₁+m+kx₂+m=k（x₁+x₂）+2m，
∴k(x1+x2)+2m-3=-

3

2

(x1+x2+2)，
∴(k+

3

2

)(x1+x2)+2m=0，
∴(k+

3

2

)×

-8km

3+4k2

+2m=0，
化为m（2k-1）=0，
若m=0，则直线AB经过原点，此时

PA

+

PB

=2

PO

，λ=2，不符合题意，因此m≠0．
∴2k-1=0，解得k=

1

2

．