题目内容
3.已知函数f(x)=2$\sqrt{3}$cos2x+2sinxcosx-m(x∈R),函数f(x)的最大值为2.(1)求实数m的值;
(2)在△ABC中,角A、B、C所对的边是a、b、c,.若A为锐角,且满足f(A)=0,sinB=3sinC,△ABC的面积为$\frac{3\sqrt{3}}{4}$,求边长a.
分析 (1)f(x)解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,利用正弦函数的值域表示出f(x)的最大值,根据最大值为2求出m的值即可;
(2)由(1)确定出的f(x)解析式,以及f(A)=0,求出A的度数,利用正弦定理化简sinB=3sinC,得到b=3c,再利用三角形面积公式列出关系式,把sinA的值代入得到bc=3,联立求出b与c的值,利用余弦定理求出a的值即可.
解答 解:(1)∵f(x)=2$\sqrt{3}$cos2x+2sinxcosx-m=$\sqrt{3}$(cos2x+1)+sin2x-m=2sin(2x+$\frac{π}{3}$)+$\sqrt{3}$-m,
∴函数f(x)在2x+$\frac{π}{3}$=$\frac{π}{2}$时取得最大值,即2+$\sqrt{3}$-m=2,
解得:m=$\sqrt{3}$;
(2)∵f(A)=0,
∴2sin(2A+$\frac{π}{3}$)=0,即sin(2A+$\frac{π}{3}$)=0,
由A为锐角,解得:A=$\frac{π}{3}$,
∵sinB=3sinC,由正弦定理得b=3c①,
∵△ABC的面积为$\frac{3\sqrt{3}}{4}$,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$bcsin$\frac{π}{3}$=$\frac{3\sqrt{3}}{4}$,即bc=3②,
联立①②,解得:b=3,c=1,
∵a2=b2+c2-2bc•cosA=32+12-2×3×1×cos$\frac{π}{3}$,
∴a=$\sqrt{7}$.
点评 此题考查了正弦、余弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
| A. | $\frac{101}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{25}{101}$ | D. | $\frac{3}{10}$ |
| A. | [0,$\frac{1}{2}$] | B. | [-3,0] | C. | [-3,e) | D. | [0,e) |
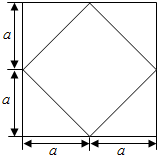 已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )
已知某个几何体的正视图、侧视图、俯视图均为如图所示的形状,根据图中标出的尺寸,可得这个几何体的体积是( )| A. | 8a3 | B. | $\frac{20}{3}$a3 | C. | 2$\sqrt{2}$a3 | D. | 5a3 |
| A. | 3(2-$\sqrt{3}$)π | B. | 4(2-$\sqrt{3}$)π | C. | 3(2+$\sqrt{3}$)π | D. | 4(2+$\sqrt{3}$)π |
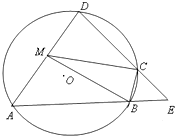 如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.