题目内容
【题目】已知各项均为正数的两个数列![]() 和{
和{![]() }满足:an+1=
}满足:an+1=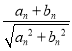 ,n∈N*.
,n∈N*.
(1)设bn+1=1+![]() ,n∈N*,求证:数列
,n∈N*,求证:数列![]() 是等差数列;
是等差数列;
(2)设bn+1=![]() ·
·![]() ,n∈N*,且
,n∈N*,且![]() 是等比数列,求a1和b1的值.
是等比数列,求a1和b1的值.
【答案】(1)见解析;(2)a1=b1=![]() .
.
【解析】试题分析:(1)由an+1=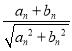 ,等式右边分子分母同时除以
,等式右边分子分母同时除以![]() ,再将bn+1=1+
,再将bn+1=1+![]() 带入可得
带入可得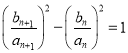 ,从而得证;
,从而得证;
(2)由不等式性质有: ![]() 进而得
进而得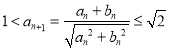 ,设等比数列{an}的公比为q,由反证法可得q=1,故an=a1(n∈N*),所以1<a1≤
,设等比数列{an}的公比为q,由反证法可得q=1,故an=a1(n∈N*),所以1<a1≤![]() ,从而得{bn}是公比为
,从而得{bn}是公比为![]() 的等比数列,亦可由反证法得a1=
的等比数列,亦可由反证法得a1=![]() .
.
试题解析:
(1)证明 由题设知an+1=![]() =
=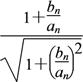 =
=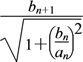 ,所以
,所以![]() =
=![]() ,
,
从而![]()
![]() -
-![]()
![]() =1(n∈N*),
=1(n∈N*),
所以数列![]() 是以1为公差的等差数列.
是以1为公差的等差数列.
(2)解 因为an>0,bn>0,
所以![]() ≤a+b<(an+bn)2,
≤a+b<(an+bn)2,
从而1<an+1=![]() ≤
≤![]() .(*)
.(*)
设等比数列{an}的公比为q,由an>0知q>0.下证q=1.
若q>1,则a1=![]() <a2≤
<a2≤![]() ,故当n>logq
,故当n>logq![]() 时,an+1=a1qn>
时,an+1=a1qn>![]() ,与(*)矛盾;
,与(*)矛盾;
若0<q<1,则a1=![]() >a2>1,故当n>logq
>a2>1,故当n>logq![]() 时,an+1=a1qn<1,与(*)矛盾.
时,an+1=a1qn<1,与(*)矛盾.
综上,q=1,故an=a1(n∈N*),
所以1<a1≤![]() .
.
又bn+1=![]() ·
·![]() =
=![]() ·bn(n∈N*),所以{bn}是公比为
·bn(n∈N*),所以{bn}是公比为![]() 的等比数列.
的等比数列.
若a1≠![]() ,则
,则![]() >1,于是b1<b2<b3.
>1,于是b1<b2<b3.
又由a1=![]() 得bn=
得bn=![]() (n∈N*),所以b1,b2,b3中至少有两项相同,矛盾,
(n∈N*),所以b1,b2,b3中至少有两项相同,矛盾,
所以a1=![]() ,从而bn=
,从而bn=![]() =
=![]() .
.
所以a1=b1=![]() .
.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案【题目】某大学志愿者协会有![]() 名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这
名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这![]() 名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为
名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为![]() .
.
性别 专业 | 中文 | 英语 | 数学 | 体育 |
男 |
|
|
|
|
女 |
|
|
|
|
现从这![]() 名同学中随机抽取
名同学中随机抽取![]() 名同学参加社会公益活动(每位同学被选到的可能性相同).
名同学参加社会公益活动(每位同学被选到的可能性相同).
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求选出的![]() 名同学恰为专业互不相同的男生的概率
名同学恰为专业互不相同的男生的概率
(Ⅲ)设![]() 为选出的
为选出的![]() 名同学中“女生或数学专业”的学生的人数,求随机变量
名同学中“女生或数学专业”的学生的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
