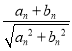题目内容
【题目】设函数f(x)=ax2-a-lnx,其中a ∈R.
(I)讨论f(x)的单调性;
(II)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数)。
【答案】(1) 当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;当
单调递减;当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增;(2)
单调递增;(2) ![]() .
.
【解析】
试题分析:本题考查导数的计算、利用导数求函数的单调性,解决恒成立问题,考查学生的分析问题、解决问题的能力和计算能力.第(Ⅰ)问,对![]() 求导,再对a进行讨论,从而判断函数
求导,再对a进行讨论,从而判断函数![]() 的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论.
的单调性;第(Ⅱ)问,利用导数判断函数的单调性,从而证明结论.
试题解析:(Ⅰ)![]()
![]()
![]() <0,
<0,![]() 在
在![]() 内单调递减.
内单调递减.
![]() 由
由![]() =0,有
=0,有![]() .
.
此时,当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;
单调递减;
当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增.
单调递增.
(Ⅱ)令![]() =
=![]() ,
,![]() =
=![]() .
.
则![]() =
=![]() .
.
而当![]() 时,
时,![]() >0,
>0,
所以![]() 在区间
在区间![]() 内单调递增.
内单调递增.
又由![]() =0,有
=0,有![]() >0,
>0,
从而当![]() 时,
时,![]() >0.
>0.
当![]() ,
,![]() 时,
时,![]() =
=![]() .
.
故当![]() >
>![]() 在区间
在区间![]() 内恒成立时,必有
内恒成立时,必有![]() .
.
当![]() 时,
时,![]() >1.
>1.
由(Ⅰ)有![]() ,从而
,从而![]() ,
,
所以此时![]() >
>![]() 在区间
在区间![]() 内不恒成立.
内不恒成立.
当![]() 时,令
时,令![]() ,
,
当![]() 时,
时,![]() ,
,
因此,![]() 在区间
在区间![]() 单调递增.
单调递增.
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
综上,![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】下表是一个容量为20的样本数据分组后的频率分布表:
分组 | [8.5,11.5] | [11.5,14.5] | [14.5,17.5] | [17.5,20.5] |
频数 | 4 | 2 | 6 | 8 |
(I)若用组中值代替本组数据的平均数,请计算样本的平均数![]() ;
;
(II)以频率估计概率,若样本的容量为2000,求在分组[14.5,17.5)中的频数;
(Ⅲ)若从数据在分组[8.5,11.5)与分组[11.5,14.5)的样本中随机抽取2个,求恰有1个样本落在分组[11.5,14.5)的概率。