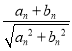题目内容
【题目】数列
满足an＝2an－1＋2n＋1(n∈N*，n≥2)， 
.
(1)求
的值；
(2)是否存在一个实数t，使得
(n∈N*)，且数列{
}为等差数列？若存在，求出实数t；若不存在，请说明理由；
(3)求数列
的前n项和
.
【答案】（1）a1＝2，a2＝9；（2）t＝1；（3）Sn＝(2n－1)×2n－n＋1.
【解析】试题分析：（1）利用an＝2an－1＋2n＋1， 
，代入可求；
（2）假设存在实数t，使得{bn}为等差数列，从而有2bn＝bn－1＋bn＋1，代入条件即可得解；
（3）利用错位相减即可得解.
试题解析：
(1)由a3＝27，得27＝2a2＋23＋1，∴a2＝9，
∵9＝2a1＋22＋1，∴a1＝2.
(2)假设存在实数t，使得{bn}为等差数列，
则2bn＝bn－1＋bn＋1(n≥2且n∈N*)，
∴2×
(an＋t)＝
(an－1＋t)＋
(an＋1＋t)，
∴4an＝4an－1＋an＋1＋t，
∴4an＝4×
＋2an＋2n＋1＋1＋t，∴t＝1.
即存在实数t＝1，使得{bn}为等差数列.
(3)由(1)，(2)得b1＝
，b2＝
，∴bn＝n＋
，
∴an＝
·2n－1＝(2n＋1)2n－1－1，
Sn＝(3×20－1)＋(5×21－1)＋(7×22－1)＋…＋[(2n＋1)×2n－1－1]
＝3＋5×2＋7×22＋…＋(2n＋1)×2n－1－n，①
∴2Sn＝3×2＋5×22＋7×23＋…＋(2n＋1)×2n－2n，②
由①－②得－Sn＝3＋2×2＋2×22＋2×23＋…＋2×2n－1－(2n＋1)×2n＋n＝1＋2×
－(2n＋1)×2n＋n
＝(1－2n)×2n＋n－1，
∴Sn＝(2n－1)×2n－n＋1.
练习册系列答案
相关题目
