题目内容

19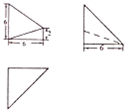．已知某空间几何体的三视图如图所示，则该几何体的体积是（　　）
A．16B．32C．36D．48

分析 根据几何体的三视图，得出该几何体为一条侧棱与底面垂直，且底面为直角梯形的四棱锥，
结合图中数据求出它的体积．

解答 解：根据几何体的三视图，得该几何体为如图所示的四棱锥，
且四棱锥的一条侧棱与底面垂直，底面为直角梯形；

其中BC=2，AD=6，AB=6，SA⊥平面ABCD，SA=6，
∴四棱锥S-ABCD的体积为
V=$\frac{1}{3}$×$\frac{1}{2}$×（2+6）×6×6=48．
故选：D．

点评 本题考查了空间三视图的应用问题，解题的关键是由三视图得出几何体的结构特征，是基础题目．

练习册系列答案
相关题目
9．已知函数g（x）=x-$\sqrt{3x+1}，h（x）=\frac{1}{2x}+\sqrt{3x+1}$，那么函数f（x）=g（x）+h（x）的解析式是f（x）=x+$\frac{1}{2x}$，（x≥-$\frac{1}{3}$，且x≠0）．
10．一次选拔运动员，测得7名选手的身高（单位：cm）分布茎叶图如图所示，已知记录的平均身高为177cm，有1名选手的身高记录不清楚，其末位数记为x，那么x的值为（　　）
A．7B．6C．5D．4
7．化简求值：
（1）tan70°cos10°（$\sqrt{3}$tan20°-1）
（2）已知cos（$\frac{π}{4}$+x）=$\frac{3}{5}$，$\frac{17π}{12}$＜x＜$\frac{7π}{4}$，求$\frac{sin2x+2si{n}^{2}x}{1-tanx}$的值．
14．某校计划新建一个占地面积为600m2的停放自行车的矩形场地，在矩形场地中间保留宽分别为2m和3m的十字型通道，如图所示，当矩形用地的边长各为多少时，自行车停放地（阴影部分）的占地面积最大？最大面积是多少？
4．复数z=（1-i）•i的共轭复数$\overline{z}$等于（　　）
A．1+iB．1-iC．-1+iD．-1-i
11．已知A，B是抛物线y2=4x上异于顶点O的两个点，直线OA与直线OB的斜率之积为定值-4，F为抛物线的焦点，△AOF，△BOF的面积分别为S1，S2，则S12+S22的最小值为（　　）
A．8B．6C．4D．2
8．已知椭圆C的焦点是F1（-2$\sqrt{2}$，0}），F2（2$\sqrt{2}$，0），其上的动点P满足|PF1|+|PF2|=4$\sqrt{3}$．点O为坐标原点，椭圆C的下顶点为R．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）设过点（0，1）且斜率为k的直线l2交椭圆C于M，N两点，试证明：无论k取何值，$\overrightarrow{RM}$•$\overrightarrow{RN}$恒为定值．
12．设x，y满足约束条件$\left\{\begin{array}{l}{x≥2}\\{3x-y≥1}\\{y≥x+1}\end{array}\right.$，若目标函数z=ax+by（a＞0，b＞0）的最小值为2，求ab的值与z的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网