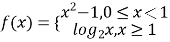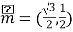题目内容
【题目】如图，A、B是海岸线OM、ON上两个码头，海中小岛有码头Q到海岸线OM、ON的距离分别为
、
，测得
，
，以点O为坐标原点，射线OM为x轴的正半轴，建立如图所示的直角坐标系，一艘游轮以
小时的平均速度在水上旅游线AB航行（将航线AB看作直线，码头Q在第一象限，航线BB经过点Q）.
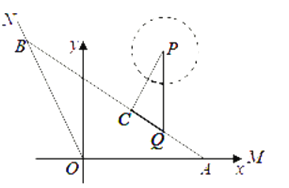
（1）问游轮自码头A沿
方向开往码头B共需多少分钟？
（2）海中有一处景点P（设点P在
平面内，
，且
），游轮无法靠近，求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
【答案】（1）30min （2）
【解析】
（1）根据已知条件，写出直线ON方程，再求解Q点坐标，由直线AQ的方程求解B点坐标，进而求解AB长.
（2）由（1）知C为垂足，可联立直线AB与PC 方程，即可求解C点坐标.
（1）由已知得，
，直线ON方程：
设
，由
及图，得
，
直线AQ的方程为
即
由
，解得
，即
，即水上旅游线AB的长为
，即30min.
（2）点P到直线AB 的垂直距离最近，则垂足为C
由（1）直线AB 方程
，则直线PC方程为
联立
，解得
练习册系列答案
相关题目
