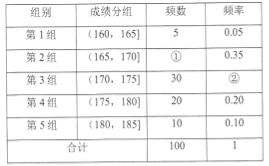
题目内容
【题目】为弘扬民族古典文化,学校举行古诗词知识竞赛,某轮比赛由节目主持人随机从题库中抽取题目让选手抢答,回答正确给改选手记正10分,否则记负10分.根据以往统计,某参赛选手能答对每一个问题的概率为![]() ;现记“该选手在回答完
;现记“该选手在回答完![]() 个问题后的总得分为
个问题后的总得分为![]() ”.
”.
(1)求![]() 且
且![]() 的概率;
的概率;
(2)记![]() ,求
,求![]() 的分布列,并计算数学期望
的分布列,并计算数学期望![]() .
.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)回答![]() 个问题总得分为
个问题总得分为![]() 分,则正确
分,则正确![]() 个,错误
个,错误![]() 个,再分情况讨论;(2)
个,再分情况讨论;(2)![]() 的取值为
的取值为![]() ,
,![]() ,
,![]() ,再算出
,再算出![]() 取每个值时的概率,写出分布列,算出期望.
取每个值时的概率,写出分布列,算出期望.
试题解析:(1)当![]() 时,即回答6个问题后,正确4个,错误2个.若回答正确第1个和第2个问题,则其余4个问题可任意回答正确2个问题;若第1个问题回答正确,第2个问题回答错误,第3个问题回答正确,则其余三个问题可任意回答正确2个.记回答每个问题正确的概率为
时,即回答6个问题后,正确4个,错误2个.若回答正确第1个和第2个问题,则其余4个问题可任意回答正确2个问题;若第1个问题回答正确,第2个问题回答错误,第3个问题回答正确,则其余三个问题可任意回答正确2个.记回答每个问题正确的概率为![]() ,则
,则![]() .同时回答每个问题错误的概率为
.同时回答每个问题错误的概率为![]() .
.
故所求概率为![]() .
.
(2)由![]() 可知
可知![]() 的取值为10,30,50.
的取值为10,30,50.
可有![]() ,
,![]()
故![]() 的分布列为:
的分布列为:
| 10 | 30 | 50 |
|
|
|
|
![]()

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目