题目内容
20.请先根据根据三视图绘制直观图.若根据已有数据可计算物体体积,请计算.
分析 根据几何体的三视图,得出该几何体是直三棱柱与直三棱锥的组合体;
结合三视图的数据特征,求出该几何体的体积.
解答 解:根据几何体的三视图,得;
该几何体是下部为直三棱柱,上部为直三棱锥的组合体;
且直三棱柱的底面三角形的底边长为2,对应边上的高是1,三棱柱的高是2;
直三棱锥与直三棱柱底面相同,高为1;
∴该几何体的体积为
V几何体=V直三棱柱+V直三棱锥
=$\frac{1}{2}$×2×1×2+$\frac{1}{3}$×$\frac{1}{2}$×2×1×1
=$\frac{7}{3}$.
点评 本题考查了利用三视图求空间几何体的体积的应用问题,也考查了空间想象能力,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.设Sn为等比数列{an}的前n项和,若8a3+a6=0,则$\frac{{S}_{6}}{{S}_{2}}$=( )
| A. | -11 | B. | -21 | C. | 11 | D. | 21 |
11.设α=2014°,则下列判断正确的是( )
| A. | sinα>0,cosα>0,tanα>0 | B. | sinα>0,cosα<0,tanα<0 | ||
| C. | sinα<0,cosα<0,tanα>0 | D. | sinα<0,cosα>0,tanα<0 |
8.若将如图的展开图还原成成正方体,则∠ABC的度数为( )
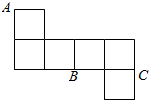

| A. | 120° | B. | 90° | C. | 60° | D. | 45° |
12.当x>0时,不等式$\frac{x}{{x}^{2}+1}$≤1-2p恒成立,则实数p的取值范围是( )
| A. | (-∞,-$\frac{1}{4}$] | B. | (-∞,$\frac{1}{4}$] | C. | [-$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |