题目内容
12.当x>0时,不等式$\frac{x}{{x}^{2}+1}$≤1-2p恒成立,则实数p的取值范围是( )| A. | (-∞,-$\frac{1}{4}$] | B. | (-∞,$\frac{1}{4}$] | C. | [-$\frac{1}{4}$,+∞) | D. | [$\frac{1}{4}$,+∞) |
分析 利用x+$\frac{1}{x}$≥2(x>0)求解,注意等号成立的条件,有条件x>0可将$\frac{x}{{x}^{2}+1}$转化求解,求出表达式的最值,即可得到p的范围.
解答 解:不等式$\frac{x}{{x}^{2}+1}$≤1-2p,
可得2p≤1-$\frac{x}{{x}^{2}+1}$=$1-\frac{1}{x+\frac{1}{x}}$,因为当x>0时,x+$\frac{1}{x}$≥2,当且仅当x=1时等号成立,
所以$\frac{1}{x+\frac{1}{x}}$$≤\frac{1}{2}$,$1-\frac{1}{x+\frac{1}{x}}≥1-\frac{1}{2}=\frac{1}{2}$,$1-\frac{1}{x+\frac{1}{x}}$的最小值为$\frac{1}{2}$,
∴实数p的取值范围是(-∞,$\frac{1}{4}$].
故选:B.
点评 本题考查了函数最值的应用、基本不等式,要注意不等式成立的条件.

练习册系列答案
相关题目
4.若α≠$\frac{kπ}{2}$(k∈Z),则f(α)=$\frac{sinα+tanα}{cosα+cotα}$的取值情况是( )
| A. | 必取正值 | B. | 必取负值 | C. | 可取零值 | D. | 可正可负 |
10.某几何体的三视图如图所示,则该几何体的体积为( )
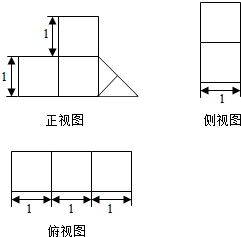

| A. | $\frac{7}{3}$ | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |
