题目内容
5.某蔬菜收购点租用车辆,将100吨新鲜黄瓜运往某市销售,可供租用的大卡车和农用车分别为10辆和20辆,若每辆卡车载重8吨,运费960元,每辆农用车载重2.5吨,运费360元,问两种车各租多少辆时,可全部运完黄瓜,且运费最低,并求出最低运费.分析 设两种车各租x,y辆时,可全部运完黄瓜,则$\left\{\begin{array}{l}{0≤x≤10}\\{0≤y≤20}\\{8x+2.5y≥100}\end{array}\right.$,运费z=960x+360y.作出可行域,直线960x+360y=0,即8x+3y=0,向上平移至过点B(10,8)时,z=960x+360y取到最小值.
解答 解:设两种车各租x,y辆时,可全部运完黄瓜,则$\left\{\begin{array}{l}{0≤x≤10}\\{0≤y≤20}\\{8x+2.5y≥100}\end{array}\right.$,
运费z=960x+360y.
作出可行域如图.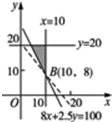
由$\left\{\begin{array}{l}{8x+2.5y=100}\\{x=10}\end{array}\right.$得B(10,8).作直线960x+360y=0,
即8x+3y=0,向上平移至过点B(10,8)时,z=960x+360y取到最小值.
z最小=960×10+360×8=12480.
所以大卡车租10辆,农用车租8辆时运费最低,最低运费为12480元.
点评 本题考查利用数学知识解决实际问题,考查线性规划知识的运用,确定可行域是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.设x∈(0,$\frac{π}{2}$),lgsin2x-lgsinx=-1,则cosx等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{20}$ | D. | $\frac{1}{40}$ |
3.设p:f(x)=ex+lnx+$\frac{1}{2}$x2+mx+2在(0,+∞)内单调递增,q:m≥-4,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |


 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段B1B,AB和A1C上的动点,观察直线CE与D1F,CE与D1G.给出下列结论: