题目内容
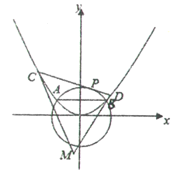
【题目】如图,已知抛物线E:![]() (
(![]() )与圆O:
)与圆O:![]() 相交于A,B两点,且
相交于A,B两点,且![]() .过劣弧
.过劣弧![]() 上的动点
上的动点![]() 作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线
作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线![]() ,
,![]() ,相交于点M.
,相交于点M.
(1)求抛物线E的方程;
(2)求点M到直线![]() 距离的最大值.
距离的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用![]() 求得圆心
求得圆心![]() 到弦
到弦![]() 的距离为1,即可求得点
的距离为1,即可求得点![]() 的坐标为
的坐标为![]() ,将
,将![]() 代入抛物线方程可得
代入抛物线方程可得![]() ,问题得解
,问题得解
(2)设![]() ,
,![]() ,分别求得
,分别求得![]() 与
与![]() 的方程,即可求得点
的方程,即可求得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,联立直线
,联立直线![]() 的方程和抛物线方程可得:
的方程和抛物线方程可得:![]() ,
,![]() ,即可得点
,即可得点![]() 的横、纵坐标为
的横、纵坐标为![]() ,
,![]() ,再由点到直线距离公式可得点M到直线
,再由点到直线距离公式可得点M到直线![]() 的距离为:
的距离为: ,
,![]() ,利用其单调性可得:
,利用其单调性可得:![]() ,问题得解
,问题得解
(1)![]()
![]() ,且B在圆上,
,且B在圆上,
所以圆心![]() 到弦
到弦![]() 的距离
的距离![]()
由抛物线和圆的对称性可得![]() ,
,
代入抛物线可得![]() ,解得
,解得![]() ,
,
∴抛物线E的方程为![]() ;
;
(2)设![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
则![]() 的方程为:
的方程为:![]() ,即
,即![]() ——①,
——①,
同理![]() 的方程为:
的方程为:![]() ——②,
——②,
联立①②解得![]() ,
,![]() ,
,
又直线![]() 与圆
与圆![]() 切于点
切于点![]() ,
,
易得![]() 方程为
方程为![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,
联立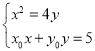 ,化简得
,化简得![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴点M到直线![]() 的距离为:
的距离为:
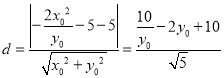 ,
,![]()
易知d关于![]() 单调递减,
单调递减,![]() ,
,
即点M到直线![]() 距离的最大值为
距离的最大值为![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目