题目内容
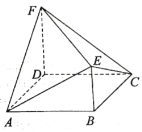
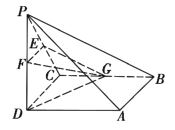
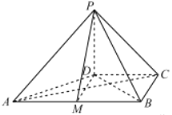
【题目】如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB//DC,AB=2CD,∠BCD=90°.
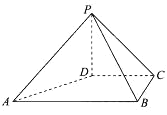
(1)求证:AD⊥PB;
(2)求点C到平面PAB的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 中点为
中点为![]() ,通过勾股定理证明
,通过勾股定理证明![]() ,再得到
,再得到![]() 平面
平面![]() ,从而证明
,从而证明![]() .
.
(2)根据三棱锥![]() 等体积转化,以
等体积转化,以![]() 为底,
为底,![]() 为高,求出三棱锥
为高,求出三棱锥![]() 的体积,再求出
的体积,再求出![]() 的面积,以
的面积,以![]() 为底,
为底,![]() 到平面
到平面![]() 的距离为高,从而得到
的距离为高,从而得到![]() 到平面
到平面![]() 的距离.
的距离.
(1)如图,取![]() 中点为
中点为![]() ,连接
,连接![]()
因为![]()
所以四边形![]() 为正方形.
为正方形.
所以![]()
所以![]() .
.
所以![]()
所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]()
(2)连接![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
则![]()
因为![]() 且
且![]()
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
在![]() 中
中![]() 即
即![]() .
.
所以![]() .
.
所以![]() .
.
所以![]() ,所以
,所以![]() .
.
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.

练习册系列答案
相关题目
【题目】某鲜花店每天制作![]() 、
、![]() 两种鲜花共
两种鲜花共![]() 束,每束鲜花的成本为
束,每束鲜花的成本为![]() 元,售价
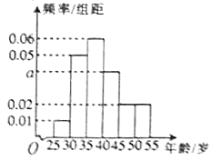
元,售价![]() 元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
元,如果当天卖不完,剩下的鲜花作废品处理.该鲜花店发现这两种鲜花每天都有剩余,为此整理了过往100天这两种鲜花的日销量(单位:束),得到如下统计数据:
| 48 | 49 | 50 | 51 |
天数 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天数 | 40 | 35 | 15 | 10 |
以这100天记录的各销量的频率作为各销量的概率,假设这两种鲜花的日销量相互独立.
(1)记该店这两种鲜花每日的总销量为![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鲜花店为了减少浪费,提升利润,决定调查每天制作鲜花的量![]() 束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与
束.以销售这两种鲜花的日总利润的期望值为决策依据,在每天所制鲜花能全部卖完与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?