题目内容
半径为1的球面上的四点A,B,C,D是正四面体的顶点，则A与B两点间的球面距离为
A．arccos(- ) | B．arccos(-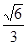 ) | C．arccos(-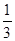 ) | D．arccos(- ) |
C
此题答案应选C
分析：由题意求出正四面体的棱长，利用余弦定理求出∠AOB，然后求出A与B两点间的球面距离．
解答：解：半径为1的球面上的四点A，B，C，D是正四面体的顶点，所以正四面体扩展为正方体的外接球与圆柱球相同，正方体的对角线就是外接球的直径，所以正四面体的棱长为：
； ()2=2-2cos∠AOB
cos∠AOB=-
A与B两点间的球面距离为：1×arccos（-）=arccos（-）
故选C．
分析：由题意求出正四面体的棱长，利用余弦定理求出∠AOB，然后求出A与B两点间的球面距离．
解答：解：半径为1的球面上的四点A，B，C，D是正四面体的顶点，所以正四面体扩展为正方体的外接球与圆柱球相同，正方体的对角线就是外接球的直径，所以正四面体的棱长为：
； ()2=2-2cos∠AOBcos∠AOB=-
A与B两点间的球面距离为：1×arccos（-
）=arccos（-）故选C．
练习册系列答案
相关题目
中，
为正方形
中心，则
与平面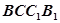
所成角的正切值为 （ ）
内的一条直线平行，则m//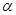
，则过
，则
为等边三角形，
为矩形，平面
平面
，
分别为
、
、
中点，
．
的体积
为两条异面直线，
为其公垂线，直线
，则
与
的顶点
在底面
内射影
在
内部，且到三个侧
，侧面积为
，则此圆锥的体积为__________
中，三组对棱棱长分别相等且依次为
、
、15，则此四面体