题目内容

9．某四棱锥的三视图如图所示，则该四棱锥的侧面积为2$\sqrt{39}$．

分析 根据几何体的三视图，得出该几何体是底面为菱形的四棱锥，画出几何体的直观图，求出它的侧面积即可．

解答 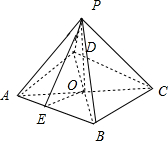解：根据几何体的三视图，得；
该几何体是底面为菱形的四棱锥，
且菱形的边长为$\sqrt{{（\sqrt{3}）}^{2}{+1}^{2}}$=2，
三棱锥的高为3，
且侧面四个三角形的面积相等，如图所示；
∴该四棱锥的侧面积为
4S△PAB=4×$\frac{1}{2}$AB•PE=4×$\frac{1}{2}$×2×$\sqrt{{3}^{2}{+（\frac{\sqrt{3}×1}{2}）}^{2}}$=2$\sqrt{39}$．
故答案为：2$\sqrt{39}$．

点评 本题考查了利用空间几何体的三视图求几何体的侧面积的应用问题，解题的关键是根据三视图得出几何体的直观图，是基础题目．

练习册系列答案
相关题目
19．如图，已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的四个顶点分别是A1，A2，B1，B2，△A2B1B2是边长为2$\sqrt{3}$的正三角形，其内切圆为圆G．
（1）求椭圆C及圆G的标准方程；
（2）若点D是椭圆C上第一象限内的动点，直线B1D交线段A2B2于点E．
（i）求$\frac{|D{B}_{1}|}{|E{B}_{1}|}$的最大值；
（ii）设F（-1，0），是否存在以椭圆C上的点M为圆心的圆M，使得过圆M上任意一点N，作圆G的切线（切点为T）都满足$\frac{|NF|}{|NT|}$=$\sqrt{2}$？若存在，请求出圆M的方程；若不存在，请说明理由．
20．如图，△ACB，△ADC都为等腰直角三角形，M为AB的中点，且平面ADC⊥平面ACB，AB=4，AC=2$\sqrt{2}$，AD=2
（1）求证：BC⊥平面ACD
（2）求直线MD与平面ADC所成的角．
17．直线l的斜率是-1，且过曲线$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=3+2sinθ}\end{array}\right.$（θ为参数）的对称中心，则直线l的方程是x+y-5=0．
4．设i为虚数单位，m∈R，“复数m（m-1）+i是纯虚数”是“m=1”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
14．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）与双曲线G：x${\;}^{2}-\frac{{y}^{2}}{3}=1$共焦点，F1，F2是双曲线的左、右焦点，P是椭圆E与双曲线G的一个交点，O为坐标原点，△PF1F2的周长为4$+4\sqrt{2}$．
（1）求椭圆E的方程；
（2）已知动直线l与椭圆E恒有两个不同交点A，B，且$\overrightarrow{OA}⊥\overrightarrow{OB}$，求△OAB面积的取值范围．
1．已知实数a，b，c，d满足a＞b＞c＞d，求证：$\frac{1}{a-b}+\frac{4}{b-c}+\frac{9}{c-d}≥\frac{36}{a-d}$．
18．在△ABC中，a、b、c分别为角A、B、C所对应的三角形的边长，若4a$\overrightarrow{BC}$+2b$\overrightarrow{CA}$+3c$\overrightarrow{AB}$=$\overrightarrow{0}$，则cosB=（　　）
A．$-\frac{29}{36}$B．$\frac{29}{36}$C．$\frac{11}{24}$D．$-\frac{11}{24}$
19．一个几何体的三视图如图所示，其中俯视图为正方形及其一条对角线，则该几何体的体积为（　　）
A．32B．48C．56D．96

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网