题目内容
20. 如图,△ACB,△ADC都为等腰直角三角形,M为AB的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2
如图,△ACB,△ADC都为等腰直角三角形,M为AB的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2(1)求证:BC⊥平面ACD
(2)求直线MD与平面ADC所成的角.
分析 (1)根据所给边的长度和△ACB,ADC都为等腰直角三角形即可知道∠ADC=90°,BC⊥AC,而根据平面ADC⊥平面ACB即可得到BC⊥平面ACD;
(2)取AC中点E,连接ME,DE,便容易说明∠EDM是直线MD与平面ADC所成的角,由已知条件即知ME=DE=$\sqrt{2}$,从而得到∠EDM=45°.
解答 解:(1)证明:根据已知条件便知∠ADC=90°,∠ACB=90°;
∴BC⊥AC;
∵平面ADC⊥平面ACB,平面ADC∩平面ACB=AC;
∴BC⊥平面ACD;
(2)如图,取AC中点E,连接ME,DE,∵M为AB中点,则: ME∥BC,ME=$\sqrt{2}$,DE=$\sqrt{2}$;
ME∥BC,ME=$\sqrt{2}$,DE=$\sqrt{2}$;
由(1)BC⊥平面ACD;
∴ME⊥平面ACD;
∴∠MDE为直线MD和平面ADC所成角;
∴在Rt△MDE中,直角边ME=DE;
∴∠MDE=45°;
即直线MD与平面ADC所成的角为45°.
点评 考查直角三角形边的关系,面面垂直的性质定理,以及中位线的性质,线面角的概念及求法.

练习册系列答案
相关题目
8.已知f(x)=$\left\{\begin{array}{l}{{x}^{2}+2014x-2015,x≤0}\\{2-x+lnx,x>0}\end{array}\right.$,则函数f(x)的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.如图是一个几何体的三视图,其中正(主)视图、侧(左)视图都是矩形,则该几何体的体积是( )
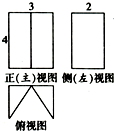

| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
12.直线y=x+4与曲线y=x2-x+1所围成的封闭图形的面积为( )
| A. | $\frac{22}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{34}{3}$ |
10.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
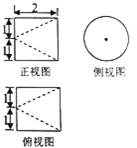

| A. | $\frac{π}{3}$cm3 | B. | $\frac{2π}{3}$cm3 | C. | πcm3 | D. | $\frac{4π}{3}$cm3 |

