题目内容
17.直线l的斜率是-1,且过曲线$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=3+2sinθ}\end{array}\right.$(θ为参数)的对称中心,则直线l的方程是x+y-5=0.分析 首先,将圆的参数方程化为普通方程然后,求解其对称中心,即圆心,再利用点斜式方程,确定直线方程.
解答 解:根据曲线$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=3+2sinθ}\end{array}\right.$(θ为参数),
得(x-2)2+(y-3)2=4,
其对称中心为(2,3),
根据点斜式方程,得
y-3=-(x-2),
∴直线l的方程x+y-5=0,
故答案为:x+y-5=0.
点评 本题重点考查了圆的参数方程、直线的点斜式方程、圆的性质等知识属于中档题.

练习册系列答案
相关题目
8.已知f(x)=$\left\{\begin{array}{l}{{x}^{2}+2014x-2015,x≤0}\\{2-x+lnx,x>0}\end{array}\right.$,则函数f(x)的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.如图是一个几何体的三视图,其中正(主)视图、侧(左)视图都是矩形,则该几何体的体积是( )
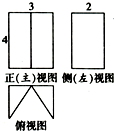

| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
12.直线y=x+4与曲线y=x2-x+1所围成的封闭图形的面积为( )
| A. | $\frac{22}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{34}{3}$ |
2.已知集合A={x|x2>1},集合B={x|x(x-2)<0},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|x>2} | C. | {x|0<x<2} | D. | {x|x≤1,或x≥2} |
6.有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
| A. | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B. | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C. | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D. | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |

 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2)则f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$).