题目内容
1．已知实数a，b，c，d满足a＞b＞c＞d，求证：$\frac{1}{a-b}+\frac{4}{b-c}+\frac{9}{c-d}≥\frac{36}{a-d}$．分析 利用柯西不等式，即可证明结论．
解答 证明：因a＞b＞c＞d，故a-b＞0，b-c＞0，c-d＞0．
故$[（a-b）+（b-c）+（c-d）]（{\frac{1}{a-b}+\frac{4}{b-c}+\frac{9}{c-d}}）≥{（1+2+3）^2}=36$，…6分
所以，$\frac{1}{a-b}+\frac{4}{b-c}+\frac{9}{c-d}≥\frac{36}{a-d}$．…10分．
点评 本题考查不等式的证明，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
12．直线y=x+4与曲线y=x2-x+1所围成的封闭图形的面积为（ ）
| A． | $\frac{22}{3}$ | B． | $\frac{28}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{34}{3}$ |
已知一个空间几何体的所有棱长均为1cm，其表面展开图如图所示，则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3．
6．有4名男医生、3名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（ ）
| A． | A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ | B． | C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | ||
| C． | C${\;}_{7}^{3}$--C${\;}_{4}^{2}$•C${\;}_{3}^{1}$ | D． | A${\;}_{7}^{3}$--A${\;}_{4}^{2}$•A${\;}_{3}^{1}$ |
10．若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（ ）
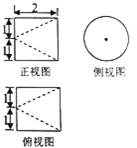
| A． | $\frac{π}{3}$cm3 | B． | $\frac{2π}{3}$cm3 | C． | πcm3 | D． | $\frac{4π}{3}$cm3 |
11．
甲、乙两名同学8次数学测验成绩如茎叶图所示，$\overline{x}$1，$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数，s1，s2分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ）
甲、乙两名同学8次数学测验成绩如茎叶图所示，$\overline{x}$1，$\overline{x}$2分别表示甲、乙两名同学8次数学测验成绩的平均数，s1，s2分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（ ）| A． | $\overline{x}$1＞$\overline{x}$2，s1＜s2 | B． | $\overline{x}$1=$\overline{x}$2，s1＜s2 | C． | $\overline{x}$1=$\overline{x}$2，s1=s2 | D． | $\overline{x}$1＜$\overline{x}$2，s1＞s2 |