题目内容
14.已知F为抛物线y2=2px(p>0)的焦点,抛物线的准线与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线分别交于A、B两点.若△AFB为直角三角形,则双曲线的离心率为$\sqrt{5}$.分析 由已知条件推导出A,B两点的纵坐标,△AFB为直角三角形,$\frac{pb}{2a}$=p,由此能求出双曲线的离心率.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),
∴双曲线的渐近线方程是y=±$\frac{b}{a}$x,
抛物线y2=2px的焦点坐标($\frac{p}{2},0$),
又∵抛物线y2=2px的准线方程为x=-$\frac{p}{2}$,
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与抛物线y2=2px的准线分别交于A,B两点,
∴A,B两点的纵坐标分别是y=$\frac{pb}{2a}$ 和y=-$\frac{pb}{2a}$,
∵△AFB为直角三角形,∴$\frac{pb}{2a}$=p,即b=2a,c2-a2=4a2,
∴e=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查抛物线解得性质以及双曲线的离心率的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
2.将函数y=sin(2x+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )
| A. | y=sin4x | B. | y=sinx | C. | y=sin(4x-$\frac{π}{6}$) | D. | y=sin(x-$\frac{π}{6}$) |
6.设F1、F2是椭圆x2+$\frac{{y}^{2}}{{b}^{2}}$=1(0<b<1)的左、右焦点,过F1的直线l交椭圆于A,B两点,若|AF1|=3|F1B|,且AF2⊥x轴,则b2=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
3.直线ax+by-a=0与圆x2+y2+2x-4=0的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 与a,b的取值有关 |
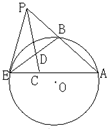 如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=75°.
如图,过点P作圆O的割线PAB与切线PE,E为切点,连接AE,BE,∠APE的平分线与AE,BE分别交于点C,D,若∠AEB=30°,则∠PCE=75°.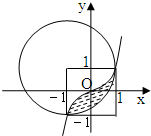 为了近似估计π的值,用计算机分别产生90个在[-1,1]的均匀随机数x1,x2,…,x90和y1,y2,…,y90,在90组数对(xi,yi)(1≤i≤90,i∈N*)中,
为了近似估计π的值,用计算机分别产生90个在[-1,1]的均匀随机数x1,x2,…,x90和y1,y2,…,y90,在90组数对(xi,yi)(1≤i≤90,i∈N*)中,