题目内容
4.四面体ABCD中,AD⊥BC,且AB+BD=AC+CD,则下列命题正确的是①③④(写出所有正确命题的编号).①由顶点D作四面体的高,其垂足为H,则AH为△ABC中BC边上的高;
②若分别作△BAD和△CAD的边AD上的高,则这两条高所在直线异面;
③若分别作△BAD和△CAD的边AD上的高,则这两条高长度相等;
④若M为AD上的动点,则均有MB=MC;
⑤AB=CD且BD=AC.
分析 ①过点D作DH⊥面ABC,由线面垂直的性质结合线面垂直的判定即可判断;
②过B在△ABD中作BO⊥AD,连接CO,运用线面垂直的判定定理和性质定理,即可判断②;
③运用空间中椭球的定义,类似平面上椭圆的定义,即可判断③;
④由直角三角形的勾股定理,结合③即可判断④;
⑤由④结合已知条件AB+BD=AC+CD,即可判断.
解答 解: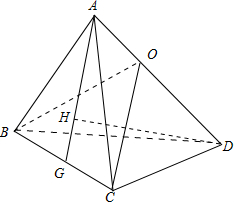 ①过点D作DH⊥面ABC,则DH⊥BC,
①过点D作DH⊥面ABC,则DH⊥BC,
又AD⊥BC,则BC⊥面ADH,AH⊥BC,
∴AH为△ABC中BC边上的高,故①正确;
②过B在△ABD中作BO⊥AD,垂足为O,连接CO,
由于AD⊥BC,又AD⊥BO,
故AD⊥平面BCO,则AD⊥CO,
即CO为边AD上的高,
显然BO,CO相交,故②错;
③在三棱锥A-BCD中,AB+BD=AC+CD>AD,
则B,C均在以A,D为焦点的椭球上,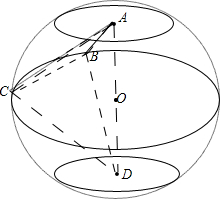 由于AD垂直于平面BCO,则AD垂直于BC,
由于AD垂直于平面BCO,则AD垂直于BC,
且B,C位于同一纬度,如图,故BO=CO,故③正确;
④在直角△MOB和直角△MOC中,BO=CO,MO=MO,
由勾股定理得,MB=MB,故④正确;
⑤在直角△ABO和直角△ACO中,BO=CO,
由勾股定理得,AB=AC,同理DB=DC,而AB+BD=AC+CD,
∴当AB≠BD时,AB≠CD且BD≠AC,故⑤错误.
故答案为:①③④.
点评 本题考查命题的真假判断与应用,主要考查空间直线与平面的位置关系,考查平面几何中的全等知识和勾股定理及运用,考查空间中到两定点的距离之和为定值的轨迹为椭球,属于难题.

练习册系列答案
相关题目
19.已知不等式xy≤ax2+2y2,若对任意x∈[1,2]及y∈[2,3],该不等式恒成立,则实数a的范围是( )
| A. | -$\frac{35}{9}$≤a≤-1 | B. | -3≤a≤-1 | C. | a≥-1 | D. | a≥-3 |
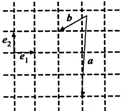 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.