题目内容
6．设F1、F2是椭圆x2+$\frac{{y}^{2}}{{b}^{2}}$=1（0＜b＜1）的左、右焦点，过F1的直线l交椭圆于A，B两点，若|AF1|=3|F1B|，且AF2⊥x轴，则b2=（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
分析 求出（-$\frac{5}{3}$c，-$\frac{1}{3}$b2），代入椭圆方程，结合1=b2+c2，即可求出椭圆的方程．
解答 解：由题意，F1（-c，0），F2（c，0），AF2⊥x轴，∴|AF2|=b2，
∴A点坐标为（c，b2），
设B（x，y），则
∵|AF1|=3|F1B|，
∴（-c-c，-b2）=3（x+c，y）
∴B（-$\frac{5}{3}$c，-$\frac{1}{3}$b2），
代入椭圆方程可得$（-\frac{5}{3}c）^{2}+\frac{（-\frac{1}{3}{b}^{2}）^{2}}{{b}^{2}}$=1，
∵1=b2+c2，
∴b2=$\frac{2}{3}$，
故选：C．
点评 本题考查椭圆的方程与性质，考查学生的计算能力，属于中档题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
16．已知函数f（x）满足f（0）=1，且对于任意实数x，y∈R都有：f（xy+1）=f（x）f（y）-f（y）-x+2，若x∈[1，3]，则$\frac{f（x-1）}{{f}^{2}（x）+1}$的最大值为（ ）
| A． | $\frac{\sqrt{2}-1}{2}$ | B． | $\frac{\sqrt{2}+1}{2}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{17}$ |
11．
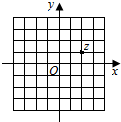若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，那么复数$\frac{z}{1+i}$对应的点位于复平面内的（ ）
若i为虚数单位，图中网格纸的小正方形的边长是1，复平面内点Z表示复数z，那么复数$\frac{z}{1+i}$对应的点位于复平面内的（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
设AB为圆O的直径，AB=10．E为线段AO上一点，OE=$\frac{1}{7}$AB．过E作一直线交圆O于C，D两点，使得∠CEA=45°．试求CE2+ED2的值．