题目内容
设S(n)=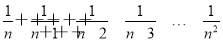 ,则( ).
,则( ).
A.S(n)共有n项,当n=2时,S(2)=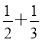
B.S(n)共有n+1项,当n=2时,S(2)=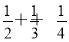
C.S(n)共有n2-n项,当n=2时,S(2)=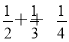
D.S(n)共有n2-n+1项,当n=2时,S(2)=
D
【解析】从n到n2共有n2-n+1个自然数,即S(n)共有n2-n+1项.

练习册系列答案
相关题目
题目内容
设S(n)=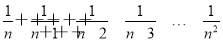 ,则( ).
,则( ).
A.S(n)共有n项,当n=2时,S(2)=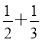
B.S(n)共有n+1项,当n=2时,S(2)=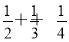
C.S(n)共有n2-n项,当n=2时,S(2)=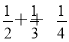
D.S(n)共有n2-n+1项,当n=2时,S(2)=
D
【解析】从n到n2共有n2-n+1个自然数,即S(n)共有n2-n+1项.
