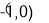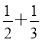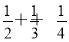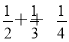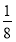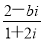题目内容
已知函数f(x)在[0,1]上有意义，且f(0)＝f(1)，如果对任意的x1，x2∈[0,1]
且x1≠x2，都有|f(x1)－f(x2)|<|x1－x2|，求证：|f(x1)－f(x2)|<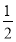
，若用反证法证明该题，则反设应为________．
存在x1，x2∈[0,1]且x1≠x2，虽然|f(x1)－f(x2)|<|x1－x2|，但|f(x1)－f(x2)|≥
【解析】根据已知和反证法的要求，反设应为：存在x1，x2∈[0,1]且x1≠x2，虽然|f(x1)－f(x2)|<|x1－x2|，但|f(x1)－f(x2)|≥
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
