题目内容
(1)已知函数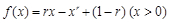 ,其中
,其中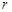 为有理数,且
为有理数,且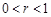 . 求
. 求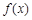 的最小值;
的最小值;
(2)试用(1)的结果证明如下命题:设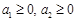 ,
,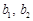 为正有理数. 若
为正有理数. 若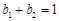 ,则
,则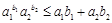 ;
;
(3)请将(2)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当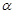 为正有理数时,有求导公式
为正有理数时,有求导公式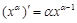 .
.
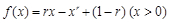 ,其中
,其中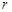 为有理数,且
为有理数,且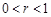 . 求
. 求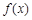 的最小值;
的最小值;(2)试用(1)的结果证明如下命题:设
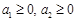 ,
,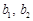 为正有理数. 若
为正有理数. 若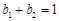 ,则
,则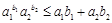 ;
;(3)请将(2)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当
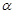 为正有理数时,有求导公式
为正有理数时,有求导公式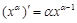 .
.(1)函数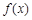 在
在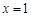 处取得最小值
处取得最小值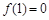 .
.
(2)见解析
(3)(2)中命题的推广形式为:设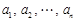 为非负实数,
为非负实数,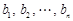 为正有理数. 若
为正有理数. 若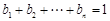 ,则
,则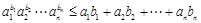
证明见解析
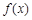 在
在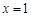 处取得最小值
处取得最小值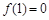 .
.(2)见解析
(3)(2)中命题的推广形式为:设
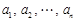 为非负实数,
为非负实数,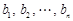 为正有理数. 若
为正有理数. 若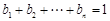 ,则
,则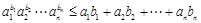
证明见解析
本题主要考察利用导数求函数的最值,并结合推理,考察数学归纳法,对考生的归纳推理能力有较高要求。
(1)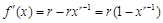 ,令
,令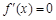 ,解得
,解得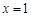 .
.
当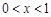 时,
时,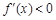 ,所以
,所以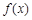 在
在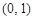 内是减函数;
内是减函数;
当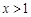 时,
时,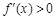 ,所以
,所以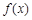 在
在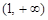 内是增函数.
内是增函数.
故函数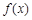 在
在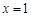 处取得最小值
处取得最小值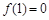 .
.
(2)由(1)知,当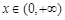 时,有
时,有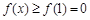 ,即
,即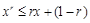 ①
①
若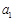 ,
,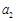 中有一个为0,则
中有一个为0,则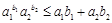 成立;
成立;
若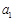 ,
,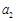 均不为0,又
均不为0,又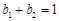 ,可得
,可得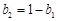 ,于是
,于是
在①中令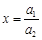 ,
,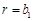 ,可得
,可得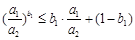 ,
,
即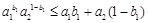 ,亦即
,亦即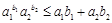 .
.
综上,对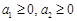 ,
,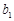 ,
,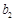 为正有理数且
为正有理数且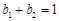 ,总有
,总有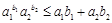 . ②
. ②
(3)(2)中命题的推广形式为:
设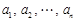 为非负实数,
为非负实数,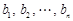 为正有理数.
为正有理数.
若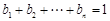 ,则
,则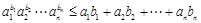 . ③
. ③
用数学归纳法证明如下:
(1)当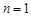 时,
时,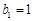 ,有
,有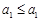 ,③成立.
,③成立.
(2)假设当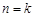 时,③成立,即若
时,③成立,即若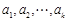 为非负实数,
为非负实数,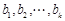 为正有理数,
为正有理数,
且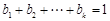 ,则
,则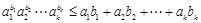 .
.
当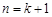 时,已知
时,已知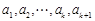 为非负实数,
为非负实数,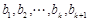 为正有理数,
为正有理数,
且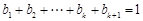 ,此时
,此时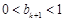 ,即
,即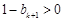 ,于是
,于是
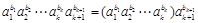 =
=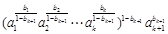 .
.
因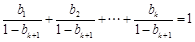 ,由归纳假设可得
,由归纳假设可得
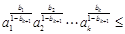
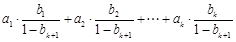
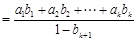 ,
,
从而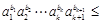
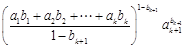 .
.
又因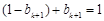 ,由②得
,由②得
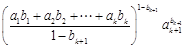
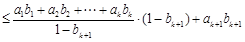
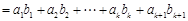 ,
,
从而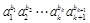
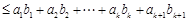 .
.
故当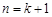 时,③成立.
时,③成立.
由(1)(2)可知,对一切正整数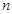 ,所推广的命题成立.
,所推广的命题成立.
说明:(3)中如果推广形式中指出③式对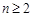 成立,则后续证明中不需讨论
成立,则后续证明中不需讨论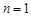 的情况.
的情况.
(1)
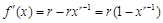 ,令
,令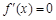 ,解得
,解得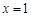 .
.当
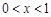 时,
时,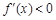 ,所以
,所以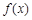 在
在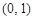 内是减函数;
内是减函数;当
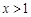 时,
时,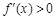 ,所以
,所以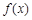 在
在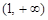 内是增函数.
内是增函数.故函数
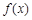 在
在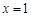 处取得最小值
处取得最小值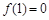 .
. (2)由(1)知,当
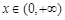 时,有
时,有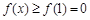 ,即
,即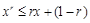 ①
①若
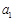 ,
,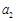 中有一个为0,则
中有一个为0,则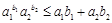 成立;
成立;若
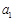 ,
,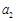 均不为0,又
均不为0,又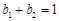 ,可得
,可得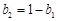 ,于是
,于是在①中令
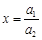 ,
,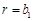 ,可得
,可得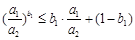 ,
,即
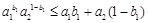 ,亦即
,亦即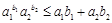 .
.综上,对
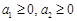 ,
,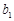 ,
,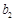 为正有理数且
为正有理数且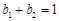 ,总有
,总有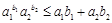 . ②
. ②(3)(2)中命题的推广形式为:
设
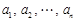 为非负实数,
为非负实数,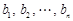 为正有理数.
为正有理数. 若
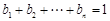 ,则
,则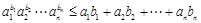 . ③
. ③用数学归纳法证明如下:
(1)当
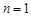 时,
时,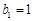 ,有
,有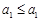 ,③成立.
,③成立. (2)假设当
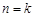 时,③成立,即若
时,③成立,即若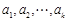 为非负实数,
为非负实数,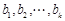 为正有理数,
为正有理数,且
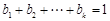 ,则
,则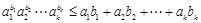 .
. 当
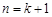 时,已知
时,已知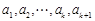 为非负实数,
为非负实数,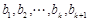 为正有理数,
为正有理数,且
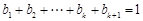 ,此时
,此时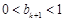 ,即
,即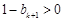 ,于是
,于是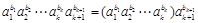 =
=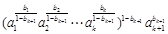 .
.因
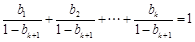 ,由归纳假设可得
,由归纳假设可得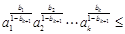
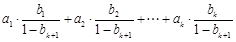
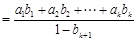 ,
,从而
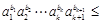
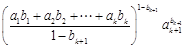 .
. 又因
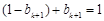 ,由②得
,由②得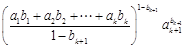
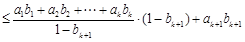
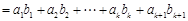 ,
,从而
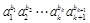
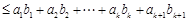 .
.故当
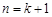 时,③成立.
时,③成立.由(1)(2)可知,对一切正整数
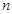 ,所推广的命题成立.
,所推广的命题成立.说明:(3)中如果推广形式中指出③式对
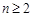 成立,则后续证明中不需讨论
成立,则后续证明中不需讨论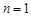 的情况.
的情况.
练习册系列答案
相关题目
 ,过曲线
,过曲线 上的点
上的点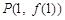 的切线斜率为3.
的切线斜率为3.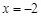 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;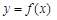 在
在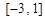 上最大值;
上最大值;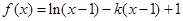
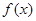 的单调区间;
的单调区间;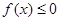 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;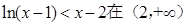 上恒成立
上恒成立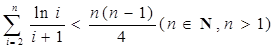
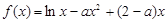 .
.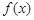 的单调性;
的单调性;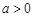 ,证明:当
,证明:当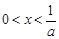 时,
时,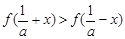 ;
;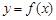 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,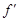 (x0)<0.
(x0)<0.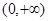 上为增函数的是 ( )
上为增函数的是 ( )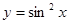
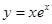
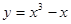
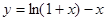
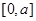 上的函数
上的函数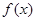 的图象如右下图所示,记以
的图象如右下图所示,记以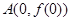 ,
,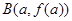 ,
,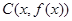 为顶点的三角形的面积为
为顶点的三角形的面积为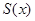 ,则函数
,则函数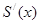 的图象大致是
的图象大致是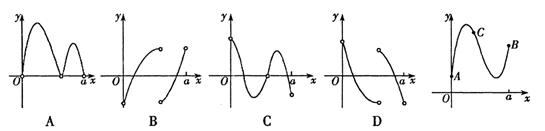
 在
在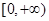 上的最小值;
上的最小值;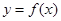 在点
在点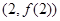 的切线方程为
的切线方程为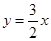 ;求
;求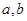 的值。
的值。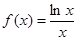 ,若方程
,若方程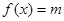 存在两个不同的实数解,则实数
存在两个不同的实数解,则实数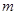 的取值范围为( ▲ )
的取值范围为( ▲ )



 在
在 上为减函数,则
上为减函数,则 的取值范围是 .
的取值范围是 .