题目内容
(本题满分14分)
(理)(1)证明不等式: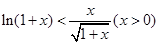
(2)已知函数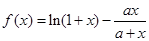 在
在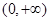 上单调递增,求实数
上单调递增,求实数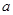 的取值范围.
的取值范围.
(3)若关于x的不等式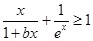 在
在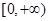 上恒成立,求实数
上恒成立,求实数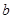 的最大值.
的最大值.
(文)已知函数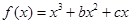 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.
(Ⅰ)求b的值;
(Ⅱ)若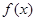 在
在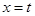 处取得极小值,记此极小值为
处取得极小值,记此极小值为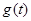 ,求
,求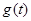 的定义域和值域.
的定义域和值域.
(理)(1)证明不等式:
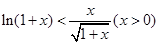
(2)已知函数
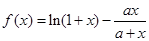 在
在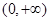 上单调递增,求实数
上单调递增,求实数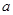 的取值范围.
的取值范围.(3)若关于x的不等式
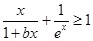 在
在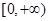 上恒成立,求实数
上恒成立,求实数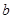 的最大值.
的最大值.(文)已知函数
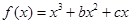 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.(Ⅰ)求b的值;
(Ⅱ)若
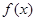 在
在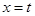 处取得极小值,记此极小值为
处取得极小值,记此极小值为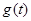 ,求
,求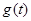 的定义域和值域.
的定义域和值域.理:(1)见解析;(2)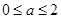 ;(3)
;(3)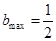 .
.
文:(1)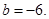 (2)定义域为
(2)定义域为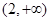 ,值域为
,值域为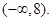
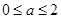 ;(3)
;(3)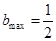 .
.文:(1)
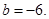 (2)定义域为
(2)定义域为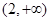 ,值域为
,值域为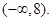
(1)两边都有变量x在证明时,如果可看作两个函数,但不能做出其图像的情况下,一般考虑构造成一个函数通过研究最值来解决,本小题显然可以构造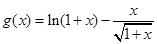 ,然后利用导数研究其最值即可证明.
,然后利用导数研究其最值即可证明.
(2)本小题解决的思路是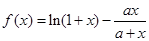 在
在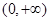 上单调递增转化为
上单调递增转化为
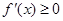 在
在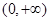 上恒成立问题解决.
上恒成立问题解决.
(3)本小题可先把参数与变量分离,基本思路是由已知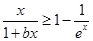 在
在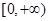 上恒成立,∵
上恒成立,∵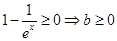 ,
,
当x>0时,易得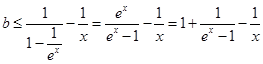 恒成立.
恒成立.
然后再研究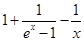 的最小值即可.
的最小值即可.
文:(1)由于f(x)的导函数是二次函数,所以x=2就是其导函数的对称轴,据此可求出b值.
(II)由(Ⅰ)知,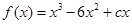 ,
,
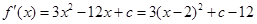 .
.
然后再分别讨论当c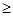 12和c<12的极值情况,从而确定其极小值,由于极小值g(t)是关于t的函数,然后再利用函数求定义域和值域的方法求解即可
12和c<12的极值情况,从而确定其极小值,由于极小值g(t)是关于t的函数,然后再利用函数求定义域和值域的方法求解即可
解:(理)(1)令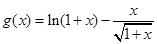 ,
,
则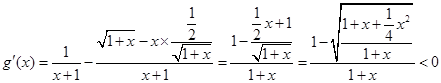
∴g(x)在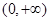 上单调递减,即g(x)<g(0),从而
上单调递减,即g(x)<g(0),从而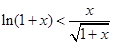 成立
成立
……………4分
(2)由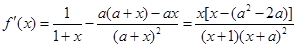 ,当x=0或
,当x=0或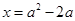 时,
时,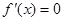 ,由已知得
,由已知得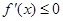 在
在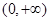 上恒成立,∴
上恒成立,∴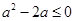 ,又f(x)在
,又f(x)在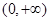 有意义,∴a≥0,综上:
有意义,∴a≥0,综上: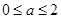 ;
;
………………8分
(3)由已知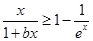 在
在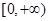 上恒成立,∵
上恒成立,∵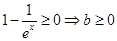 ,
,
当x>0时,易得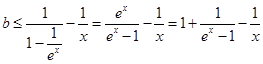 恒成立,……10分
恒成立,……10分
令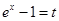 得
得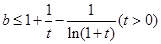 恒成立,由(2)知:令a=2得:
恒成立,由(2)知:令a=2得: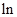 (1+x)>
(1+x)>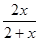 ,∴
,∴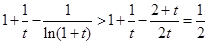 ; …………12分
; …………12分
由(1)得: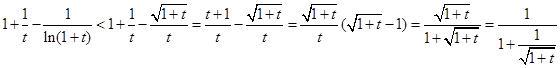 当
当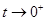 时,
时,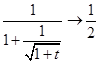 ;∴当
;∴当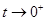 时,
时,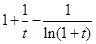 不大于
不大于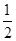 ;∴
;∴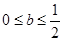 ;
;
当x=0时,b∈R,综上: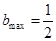 ………14分
………14分
解:(文)(Ⅰ)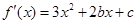 .因为函数
.因为函数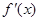 的图象关于直线x=2对称,所以
的图象关于直线x=2对称,所以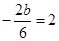 ,于是
,于是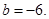 ………………2分
………………2分
(Ⅱ)由(Ⅰ)知,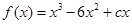 ,
,
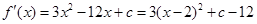 . ………4分
. ………4分
(ⅰ)当c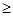 12时,
12时,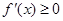 ,此时
,此时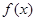 无极值. ………6分
无极值. ………6分
(ii)当c<12时,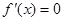 有两个互异实根
有两个互异实根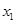 ,
,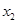 .不妨设
.不妨设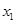 <
<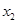 ,则
,则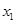 <2<
<2<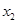 .
.
当x<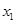 时,
时,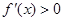 ,
,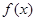 在区间
在区间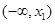 内为增函数;
内为增函数;
当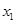 <x<
<x<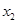 时,
时,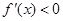 ,
,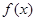 在区间
在区间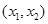 内为减函数;
内为减函数;
当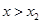 时,
时,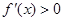 ,
,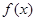 在区间
在区间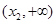 内为增函数.
内为增函数.
所以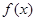 在
在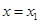 处取极大值,在
处取极大值,在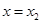 处取极小值. ………10分
处取极小值. ………10分
因此,当且仅当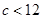 时,函数
时,函数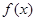 在
在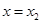 处存在唯一极小值,所以
处存在唯一极小值,所以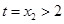 .
.
于是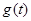 的定义域为
的定义域为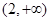 .由
.由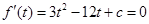 得
得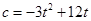 .
.
于是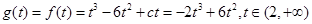 . ………12分
. ………12分
当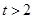 时,
时,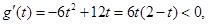 所以函数
所以函数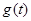 在区间
在区间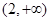 内是减函数,故
内是减函数,故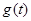 的值域为
的值域为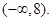 ………14分
………14分
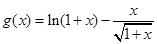 ,然后利用导数研究其最值即可证明.
,然后利用导数研究其最值即可证明.(2)本小题解决的思路是
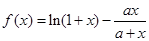 在
在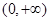 上单调递增转化为
上单调递增转化为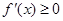 在
在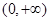 上恒成立问题解决.
上恒成立问题解决.(3)本小题可先把参数与变量分离,基本思路是由已知
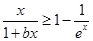 在
在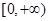 上恒成立,∵
上恒成立,∵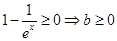 ,
,当x>0时,易得
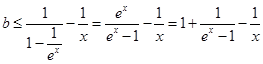 恒成立.
恒成立.然后再研究
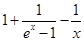 的最小值即可.
的最小值即可.文:(1)由于f(x)的导函数是二次函数,所以x=2就是其导函数的对称轴,据此可求出b值.
(II)由(Ⅰ)知,
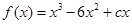 ,
,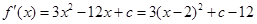 .
. 然后再分别讨论当c
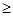 12和c<12的极值情况,从而确定其极小值,由于极小值g(t)是关于t的函数,然后再利用函数求定义域和值域的方法求解即可
12和c<12的极值情况,从而确定其极小值,由于极小值g(t)是关于t的函数,然后再利用函数求定义域和值域的方法求解即可解:(理)(1)令
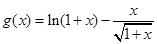 ,
,则
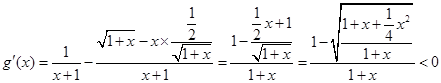
∴g(x)在
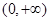 上单调递减,即g(x)<g(0),从而
上单调递减,即g(x)<g(0),从而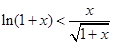 成立
成立……………4分
(2)由
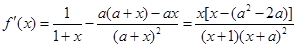 ,当x=0或
,当x=0或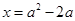 时,
时,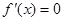 ,由已知得
,由已知得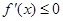 在
在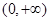 上恒成立,∴
上恒成立,∴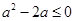 ,又f(x)在
,又f(x)在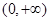 有意义,∴a≥0,综上:
有意义,∴a≥0,综上: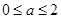 ;
;………………8分
(3)由已知
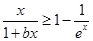 在
在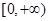 上恒成立,∵
上恒成立,∵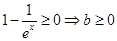 ,
,当x>0时,易得
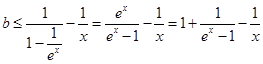 恒成立,……10分
恒成立,……10分令
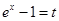 得
得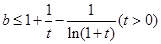 恒成立,由(2)知:令a=2得:
恒成立,由(2)知:令a=2得: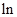 (1+x)>
(1+x)>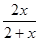 ,∴
,∴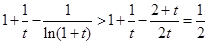 ; …………12分
; …………12分由(1)得:
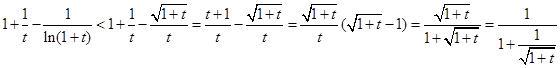 当
当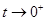 时,
时,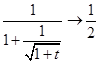 ;∴当
;∴当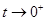 时,
时,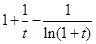 不大于
不大于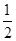 ;∴
;∴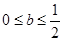 ;
;当x=0时,b∈R,综上:
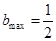 ………14分
………14分解:(文)(Ⅰ)
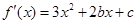 .因为函数
.因为函数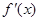 的图象关于直线x=2对称,所以
的图象关于直线x=2对称,所以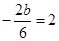 ,于是
,于是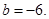 ………………2分
………………2分(Ⅱ)由(Ⅰ)知,
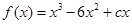 ,
,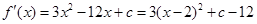 . ………4分
. ………4分(ⅰ)当c
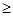 12时,
12时,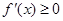 ,此时
,此时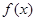 无极值. ………6分
无极值. ………6分(ii)当c<12时,
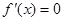 有两个互异实根
有两个互异实根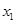 ,
,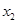 .不妨设
.不妨设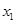 <
<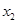 ,则
,则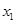 <2<
<2<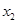 .
.当x<
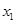 时,
时,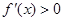 ,
,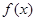 在区间
在区间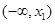 内为增函数;
内为增函数;当
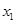 <x<
<x<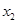 时,
时,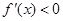 ,
,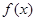 在区间
在区间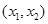 内为减函数;
内为减函数;当
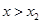 时,
时,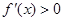 ,
,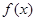 在区间
在区间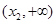 内为增函数.
内为增函数. 所以
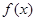 在
在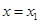 处取极大值,在
处取极大值,在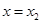 处取极小值. ………10分
处取极小值. ………10分因此,当且仅当
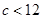 时,函数
时,函数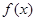 在
在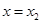 处存在唯一极小值,所以
处存在唯一极小值,所以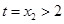 .
.于是
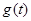 的定义域为
的定义域为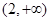 .由
.由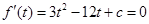 得
得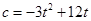 .
.于是
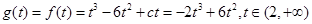 . ………12分
. ………12分当
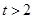 时,
时,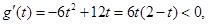 所以函数
所以函数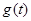 在区间
在区间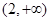 内是减函数,故
内是减函数,故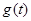 的值域为
的值域为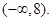 ………14分
………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
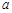 为实数,
为实数,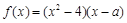 ,
,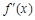 为
为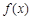 的导函数.
的导函数.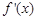 ;
;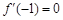 ,求
,求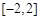 上的最大值和最小值;
上的最大值和最小值;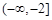 和
和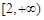 上都是递增的,求
上都是递增的,求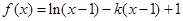
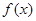 的单调区间;
的单调区间;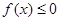 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;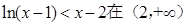 上恒成立
上恒成立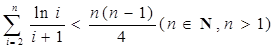
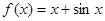
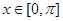 时,求
时,求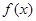 的值域
的值域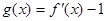 ,若
,若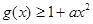 在
在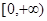 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围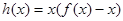 ,若
,若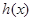 在
在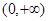 上的所有极值点按从小到大排成一列
上的所有极值点按从小到大排成一列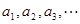 ,
,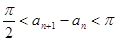
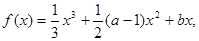 (
(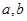 为常数)在
为常数)在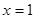 和
和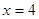 处取得极值,
处取得极值,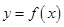 的解析式;
的解析式;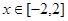 时,
时,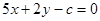 的下方,求实数
的下方,求实数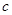 的取值范围.
的取值范围. ,曲线
,曲线 过P(1,0),且在P点处的切斜线率为2.
过P(1,0),且在P点处的切斜线率为2. .
.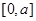 上的函数
上的函数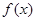 的图象如右下图所示,记以
的图象如右下图所示,记以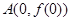 ,
,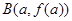 ,
,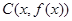 为顶点的三角形的面积为
为顶点的三角形的面积为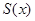 ,则函数
,则函数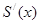 的图象大致是
的图象大致是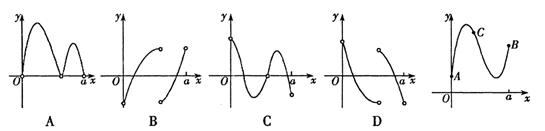
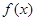 是定义在区间
是定义在区间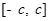 (
(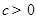 )上的奇函数,令
)上的奇函数,令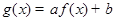 ,并有关于函数
,并有关于函数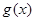 的四个论断:
的四个论断: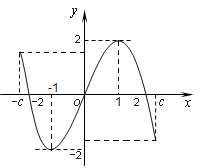
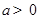 ,对于
,对于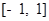 内的任意实数
内的任意实数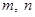 (
(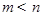 ),
),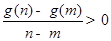 恒成立;
恒成立;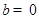 ;
;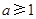 ,
,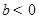 ,则方程
,则方程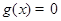 必有3个实数根;
必有3个实数根;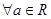 ,
,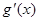 有两个零点;
有两个零点; 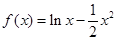 的大致图像是( )
的大致图像是( )