题目内容
【题目】已知双曲线![]() 的焦点在
的焦点在![]() 轴上,虚轴长为4,且与双曲线
轴上,虚轴长为4,且与双曲线![]() 有相同渐近线.
有相同渐近线.
(1)求双曲线![]() 的方程.
的方程.
(2)过点![]() 的直线
的直线![]() 与双曲线的异支相交于
与双曲线的异支相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)根据有相同的渐近线可设所求双曲线为![]() ,再利用焦点位置及虚轴长即可求出双曲线方程(2)根据题意知直线不能为x轴,设直线方程为
,再利用焦点位置及虚轴长即可求出双曲线方程(2)根据题意知直线不能为x轴,设直线方程为![]() ,联立双曲线方程,根据直线与双曲线的位置关系及三角形面积公式
,联立双曲线方程,根据直线与双曲线的位置关系及三角形面积公式![]() 可求出m,写出直线方程即可.
可求出m,写出直线方程即可.
(1)![]() 与双曲线
与双曲线![]() 有相同渐近线,
有相同渐近线,
![]() 设所求双曲线为
设所求双曲线为![]() ,
,
即![]() ,
,
![]() 焦点在
焦点在![]() 轴上,虚轴长为4,
轴上,虚轴长为4,
![]() ,解得
,解得![]() ,
,
故双曲线![]() 的方程为
的方程为![]()
(2)由题意知直线斜率不为0,
设直线方程为![]() ,
,
联立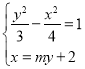 ,
,
消元得:![]() ,
,
![]() 直线
直线![]() 与双曲线的异支相交于
与双曲线的异支相交于![]() 两点,
两点,
![]() ,
,
设![]() ,
,
则![]() ,
,
且![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
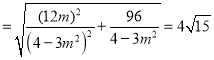 ,
,
 ,
,
化简得:![]() ,
,
![]() ,
,
令![]() ,
,
则![]() ,
,
得:![]() 或
或![]() ,
,
由![]() ,即
,即![]() 知,
知,![]() 不符合题意,
不符合题意,
![]() ,即
,即![]()
解得:![]() ,
,
此时![]() 满足
满足![]() ,
,![]() ,
,
故所求直线方程为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】小明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):
场次 | 投篮次数 | 命中次数 |
主场1 | 22 | 12 |
主场2 | 15 | 12 |
主场3 | 12 | 8 |
主场4 | 23 | 8 |
主场5 | 24 | 20 |
场次 | 投篮次数 | 命中次数 |
客场1 | 18 | 8 |
客场2 | 13 | 12 |
客场3 | 21 | 7 |
客场4 | 18 | 15 |
客场5 | 25 | 12 |
(1)从上述比赛中随机选择一场,求小明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求小明的投篮命中率一场超过0.6,一场不超过0.6的概率.