题目内容
18.设函数f(x)=$\left\{\begin{array}{l}{-1,-2≤x≤0}\\{x-1,0<x≤2}\end{array}\right.$,若函数g(x)=f(x)-ax(-2≤x≤2)是偶函数,则f[g(a)]=-1.分析 依题意,可求得g(x)=$\left\{\begin{array}{l}-ax-1,-2≤x≤0\\(1-a)x-1,0<x≤2\end{array}\right.$,依题意,g(-1)=g(1)即可求得实数a的值,代入要可得答案..
解答 解:∵f(x)=$\left\{\begin{array}{l}-1,-2≤x≤0\\ x-1,0<x≤2\end{array}\right.$,
∴g(x)=f(x)-ax=$\left\{\begin{array}{l}-ax-1,-2≤x≤0\\(1-a)x-1,0<x≤2\end{array}\right.$,
∵g(x)在-2≤x≤2时为偶函数,
∴g(-1)=g(1),即a-1=1-a-1=-a,
∴2a=1,
∴a=$\frac{1}{2}$.
∴g(x)=$\left\{\begin{array}{l}-\frac{1}{2}x-1,-2≤x≤0\\ \frac{1}{2}x-1,0<x≤2\end{array}\right.$
∴f[g($\frac{1}{2}$)]=f($\frac{1}{2}×\frac{1}{2}-1$)=f(-$\frac{3}{4}$)=-1,
故答案为:-1.
点评 本题考查函数奇偶性的性质,求得g(x)的解析式后,利用特值法g(-1)=g(1)是解决问题的关键,属于中档题.

练习册系列答案
相关题目
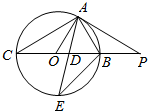 如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.
如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.