题目内容
10.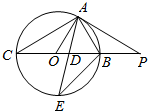 如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.
如图,已知直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),若PA=3,PB=1.(1)求sin∠PAB的大小;
(2)若∠BAC的平分线与BC交于点D,与⊙O的另一个交点为E,求AD•DE.
分析 (1)利用△PAB∽△PCA,可得$\frac{PA}{PC}=\frac{PB}{PA}=\frac{AB}{CA}$,结合PA=3,PB=1,可得$\frac{AB}{CA}$=$\frac{1}{3}$,即可求sin∠PAB的大小;
(2)利用角平分线的性质,可得$\frac{AB}{CA}$=$\frac{DB}{CD}$=$\frac{1}{3}$,求出BC,可得DB,CD,利用相交弦定理,即可求AD•DE.
解答 解:(1)∵直线PA与⊙O切于点A,直线PB过圆心O,且与⊙O交于点B、C(PB<PC),
∴∠PAB=∠ACB
∴△PAB∽△PCA,
∴$\frac{PA}{PC}=\frac{PB}{PA}=\frac{AB}{CA}$,
∵PA=3,PB=1,
∴$\frac{AB}{CA}$=$\frac{1}{3}$,
∴sin∠ACB=$\frac{\sqrt{10}}{10}$,
∴sin∠PAB=$\frac{\sqrt{10}}{10}$;
(2)由角平分线的性质,可得$\frac{AB}{CA}$=$\frac{DB}{CD}$=$\frac{1}{3}$,
∵PA2=PB•PC,∴PC=9,
∴BC=8,
∴DB=2,CD=6,
∴AD•DE=DB•CD=12.
点评 本题考查三角形相似的判定与性质,考查角平分线的性质、相交弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目