题目内容
3.已知函数f(x)=$\frac{{x}^{2}+ax+11}{x+1}$(x∈N*),且[f(x)]min=3,则实数a的取值集合是[-$\frac{8}{3}$,+∞).分析 利用f(x)=$\frac{{x}^{2}+ax+11}{x+1}$(x∈N*),且[f(x)]min=3,可得x2+ax+11≥3x+3恒成立,分离参数可得a≥-$\frac{8}{x}$-x+3恒成立,求出右边的最小值,即可求出实数a的取值集合.
解答 解:∵f(x)=$\frac{{x}^{2}+ax+11}{x+1}$(x∈N*),且[f(x)]min=3,
∴x2+ax+11≥3x+3恒成立,
∴ax≥-x2-8+3x,又x∈N*,
∴a≥-$\frac{8}{x}$-x+3恒成立,
再令h(x)=x+$\frac{8}{x}$(x∈N*),
∵h(x)=x+$\frac{8}{x}$在(0,2$\sqrt{2}$]上单调递减,在[2$\sqrt{2}$,+∞)上单调递增,而x∈N*,
∴h(x)在x取距离2$\sqrt{2}$较近的整数值时达到最小,而距离2$\sqrt{2}$较近的整数为2和3,
∵h(2)=6,h(3)=$\frac{17}{3}$,h(2)>h(3),
∴当x∈N*时,h(x)min=$\frac{17}{3}$.
∴a≥-$\frac{8}{3}$.
故答案为:[-$\frac{8}{3}$,+∞).
点评 本题考查函数恒成立问题,考查函数的最小值,正确分离参数是关键.

练习册系列答案
相关题目
12.下列选项正确的是( )
| A. | p(A|B)=P(B|A) | B. | P(A∩B|A)=P(B) | C. | $\frac{P(AB)}{P(B)}$=P(B|A) | D. | p(A|B)=$\frac{n(AB)}{n(B)}$ |
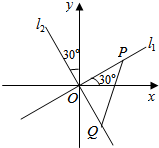 如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.