题目内容
7.已知数列{an}的前n项和为Sn,且Sn=tan-t,n∈N*,t∈R.(Ⅰ)若数列{an}为等比数列,求t的取值范围和此时数列{an}的通项公式;
(Ⅱ)若t=2,且2bn=a2n-1,证明:{bn}为等差数列,并求数列{anbn}的前n项和Tn.
分析 (I)利用递推式与等比数列的通项公式即可得出;
(II)利用(I)可得bn,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 (Ⅰ)解:(ⅰ)当n=1时,由Sn=tan-t,①,得a1=S1=ta1-t,
由数列{an}为等比数列,知t≠1且t≠0,此时${a_1}=\frac{t}{t-1}$,
(ⅱ)当n≥2时,Sn-1=tan-1-t,②,①-②得:Sn-Sn-1=t(an-an-1)=an,
即(t-1)an=tan-1,∵t≠1且t≠0,
∴${a_n}=\frac{t}{t-1}{a_{n-1}}$,结合${a_1}=\frac{t}{t-1}$,知等比数列{an}的通项公式为${a_n}={(\frac{t}{t-1})^n}$,t的取值范围是t≠1且t≠0.
(Ⅱ)证明:当t=2时,由(Ⅰ)得${a_n}={2^n}$,∴${2^{b_n}}={a_{2n-1}}={2^{2n-1}}$,得bn=2n-1,
从而bn+1-bn=2,即数列{bn}是公差为2的等差数列,
∴${a_n}{b_n}=(2n-1){2^n}$,
${T_n}=1×2+3×{2^2}+5×{2^3}+…+(2n-1){2^n}$③
$2{T_n}=1×{2^2}+3×{2^3}+5×{2^4}+…+(2n-1){2^{n+1}}$④
③-④得$-{T_n}=2+{2^3}+{2^4}+…+{2^{n+1}}-(2n-1){2^{n+1}}=2+\frac{{{2^3}(1-{2^{n-1}})}}{1-2}-(2n-1){2^{n+1}}$,
整理得${T_n}=(2n-3){2^{n+1}}+6$.
点评 本题考查了递推式的应用、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

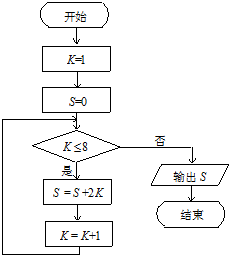
| A. | 42 | B. | 56 | C. | 72 | D. | 90 |
| A. | -ln(-x)+1 | B. | ln(-x)+1 | C. | -ln(-x)-1 | D. | ln(-x)-1 |
| A. | c>b>a | B. | b>a>c | C. | a>c>b | D. | a>b>c |
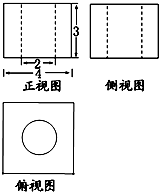
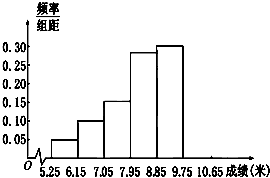 某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.
某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.