题目内容

16．函数f（x）=$\frac{1}{\sqrt{{x}^{2}-3x+2}}$+lg[1-（$\frac{1}{3}$）x]的定义域用区间表示为（0，1）∪（2，+∞）．

分析 由原函数有意义转化为求解不等式组，然后分别求解二次不等式和指数不等式，取交集后得答案．

解答 解：要使原函数有意义，则$\left\{\begin{array}{l}{{x}^{2}-3x+2＞0①}\\{1-（\frac{1}{3}）^{x}＞0②}\end{array}\right.$，
由①得，（x-1）（x-2）＞0，即x＜1或x＞2；
由②得，$（\frac{1}{3}）^{x}＜1=（\frac{1}{3}）^{0}$，即x＞0．
∴不等式组的解集为（0，1）∪（2，+∞）．
即原函数的定义域为（0，1）∪（2，+∞）．
故答案为：（0，1）∪（2，+∞）．

点评 本题考查了函数的定义域及其求法，考查了二次不等式和指数不等式的解法，是基础的计算题．

练习册系列答案
相关题目
6．某单位举办抽奖活动．已知抽奖盒中装有“天府卡，．和“熊猫卡”各两张．抽奖规则是：抽到一张“天府卡”记1分，抽到一张“熊猫卡”记2分；从盒中随机抽取两张卡片，若抽取的两张卡片所记分数之和大于或等于3分就获奖．否则就不能获奖．
（Ⅰ）参与者第一次从盒中抽取一张卡片，不放回盒中，第二次再抽取一张，求该参与者获奖的概率；
（Ⅱ）参与者第一次从盒中抽取一张卡片，放回盒中后，第二次再抽取一张．求该参与者获奖的概率．
7．已知数列{an}的前n项和为Sn，且Sn=tan-t，n∈N*，t∈R．
（Ⅰ）若数列{an}为等比数列，求t的取值范围和此时数列{an}的通项公式；
（Ⅱ）若t=2，且2bn=a2n-1，证明：{bn}为等差数列，并求数列{anbn}的前n项和Tn．
4．直角坐标系中曲线C的参数方程为$\left\{\begin{array}{l}x=4cosθ\\ y=2sinθ\end{array}$（θ为参数）．
（1）求曲线C的直角坐标方程；
（2）经过点M（2，1）作直线l交曲线C于A，B两点，若M恰好为线段AB的三等分点，求直线l的斜率．
11．如图是在竖直平面内的一个“通道游戏”．图中竖直线段和斜线段都表示通道，并且在交点处相遇，若竖直线段有第一条的为第一层，有二条的为第二层，…，依此类推．现有一颗小弹子从第一层的通道里向下运动．若在通道的分叉处，小弹子以相同的概率落入每个通道，记小弹子落入第n层第m个竖直通道（从左至右）的概率为P（n，m）．某研究性学习小组经探究发现小弹子落入第n层的第m个通道的次数服从二项分布，请你解决下列问题．
（Ⅰ）求P（2，1），P（3，2）及P（4，2）的值，并猜想P（n，m）的表达式．（不必证明）
（Ⅱ）设小弹子落入第6层第m个竖直通道得到分数为ξ，其中ξ=$\left\{\begin{array}{l}{4-m，1≤m≤3}\\{m-3，4≤m≤6}\end{array}\right.$，试求ξ的分布列及数学期望．
2．已知a∈R，函数f（x）=lnx-a（x-1），e为自然对数的底数．
（1）若a=$\frac{1}{e-1}$，求函数y=|f（x）|取得极值时所对应的x的值；
（2）若不等式f（x）≤-$\frac{a{x}^{2}}{{e}^{2}}$+$\frac{（1+2a-ea）x}{e}$恒成立，求a的取值范围．
9．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
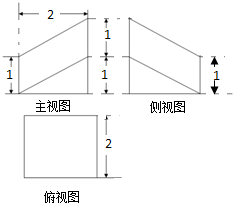
A．$\frac{14}{3}$B．4C．$\frac{10}{3}$D．3
6．已知函数f（x）=e-x（x2+ax）在点（0，f（0））处的切线斜率为2．
（Ⅰ）求实数a的值；
（Ⅱ）设g（x）=-x（x-t-$\frac{3}{e}$）（t∈R），若g（x）≥f（x）对x∈[0，1]恒成立，求t的取值范围；
（Ⅲ）已知数列{an}满足a1=1，an+1=（1+$\frac{1}{n}$）an，
求证：当n≥2，n∈N时 f（$\frac{{a}_{1}}{n}$）+f（$\frac{{a}_{2}}{n}$）+L+f（$\frac{{a}_{n-1}}{n}$）＜n•（$\frac{1}{6}+\frac{3}{2e}$）（e为自然对数的底数，e≈2.71828）．
7．函数f（x）=$\frac{2co{s}^{2}（x-1）-x}{x-1}$，其图象的对称中心是（　　）
A．（-1，1）B．（1，-1）C．（0，1）D．（0，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网