题目内容
△ABC的两个顶点为A(-4,0),B(4,0),△ABC周长为18,则C点轨迹为( )
A.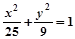 (y≠0) (y≠0) | B.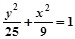 (y≠0) (y≠0) |
C.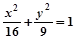 (y≠0) (y≠0) | D.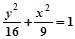 (y≠0) (y≠0) |
A
解析试题分析:由题意可得CB+AC=10>BA,故顶点C的轨迹是以B、A为焦点的椭圆,除去与x轴的交点,利用椭圆的定义和,简单性质 求出a、b 的值,即得顶点A的轨迹方程.即可知∴2a=10,c=4∴b=3,故顶点C的轨迹方程为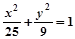 ,(y≠0),故选A.
,(y≠0),故选A.
考点:椭圆的定义
点评:本题考查椭圆的定义、标准方程,以及简单性质的应用,注意轨迹方程中y≠0,这是解题的易错点.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若双曲线 与直线
与直线 无交点,则离心率
无交点,则离心率 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线交双曲线右支于点
的切线交双曲线右支于点 ,切点为
,切点为 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C. | D. |
已知椭圆 与曲线
与曲线 的离心率互为倒数,则
的离心率互为倒数,则 ( )
( )
| A.16 | B. | C. | D. |
方程 的曲线是( )
的曲线是( )
| A.一个点 | B.一条直线 | C.两条直线 | D.一个点和一条直线 |
 的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为
的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为



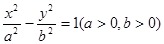 的右焦点F,作渐近线
的右焦点F,作渐近线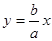 的垂线与双曲线左右两支都相交,则双曲线的离心率
的垂线与双曲线左右两支都相交,则双曲线的离心率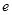 的取值范围为 ( )
的取值范围为 ( ) 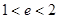
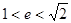
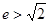
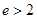





 与抛物线
与抛物线 相交于
相交于 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若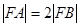 ,则k的值为( )。
,则k的值为( )。


