题目内容
设P为椭圆上一点,且∠PF1F2=30o,∠PF2F1=45o,其中F1,F2为椭圆的两个焦点,则椭圆的离心率e的值等于( )
A. | B. |
C. | D. |
C
解析试题分析:设|PF1|=x,则|PF2|=2a-x,在三角形PF1F2中,由正弦定理得 ,
,
由正弦定理得, ,
, ,所以,2a-
,所以,2a- =
= ,解得,
,解得, =
= ,故选C。
,故选C。
考点:本题主要考查椭圆的定义及其几何性质,正弦定理的应用。
点评:中档题,涉及椭圆的焦点三角形问题,一般要利用椭圆的定义。本题利用椭圆的定义及正弦定理,建立了a,c的方程,求得离心率。

练习册系列答案
相关题目
椭圆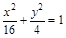 上的点到直线
上的点到直线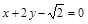 的最大距离是( )
的最大距离是( )
| A.3 | B.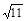 | C.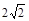 | D.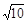 |
△ABC的两个顶点为A(-4,0),B(4,0),△ABC周长为18,则C点轨迹为( )
A.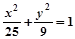 (y≠0) (y≠0) | B.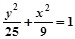 (y≠0) (y≠0) |
C.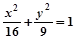 (y≠0) (y≠0) | D.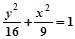 (y≠0) (y≠0) |
过M(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( )条
| A.0 | B.1 | C.2 | D.4 |
已知双曲线 与抛物线
与抛物线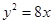 有一个公共的焦点
有一个公共的焦点 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若 ,则双曲线的渐近线方程为.
,则双曲线的渐近线方程为.
A. | B. | C. | D. |
已知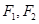 为椭圆
为椭圆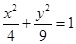 两个焦点,
两个焦点, 为椭圆上一点且
为椭圆上一点且 ,则
,则 ( )
( )
| A.3 | B.9 | C.4 | D.5 |
抛物线 的焦点坐标是
的焦点坐标是
A. | B. | C. | D. |
 的焦点为
的焦点为 ,
, ,在长轴
,在长轴 上任取一点
上任取一点 ,过
,过 ,则使得
,则使得 的点
的点
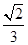


 中,
中, 分别是
分别是 的中点,以
的中点,以 为焦点且过
为焦点且过 ,则下列关于
,则下列关于


