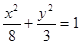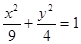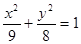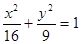题目内容
已知直线
 与抛物线
与抛物线 相交于
相交于 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若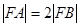 ,则k的值为( )。
,则k的值为( )。
A. | B. | C. | D. |
D
解析试题分析:抛物线C:y2=8x的准线为l:x=-2,直线y=k(x+2)(k>0)恒过定点P(-2,0)
如图过A、B分别作AM⊥l于M,BN⊥l于N,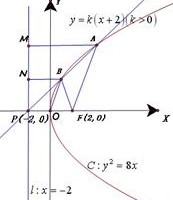
由|FA|=2|FB|,则|AM|=2|BN|,点B为AP的中点、连接OB,则|OB|= |AF|,
|AF|,
∴|OB|=|BF|,点B的横坐标为1,故点B的坐标为(1,2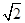 )∴k=
)∴k=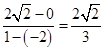 ,故选D。
,故选D。
考点:本题主要考查抛物线的定义及其几何性质。
点评:中档题,抛物线上的点,到焦点的距离与到准线的距离相等。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点 是双曲线
是双曲线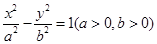 和圆
和圆 的一个交点,
的一个交点, 是双曲线的两个焦点,
是双曲线的两个焦点, ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C.2 | D. |
△ABC的两个顶点为A(-4,0),B(4,0),△ABC周长为18,则C点轨迹为( )
A.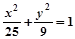 (y≠0) (y≠0) | B.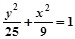 (y≠0) (y≠0) |
C.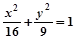 (y≠0) (y≠0) | D.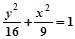 (y≠0) (y≠0) |
过M(2,4)作直线与抛物线y2=8x只有一个公共点,这样的直线有( )条
| A.0 | B.1 | C.2 | D.4 |
已知双曲线 与抛物线
与抛物线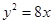 有一个公共的焦点
有一个公共的焦点 ,且两曲线的一个交点为
,且两曲线的一个交点为 ,若
,若 ,则双曲线的渐近线方程为.
,则双曲线的渐近线方程为.
A. | B. | C. | D. |
双曲线 的离心率
的离心率 ,则k的取值范围是( )
,则k的取值范围是( )
A.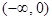 | B. | C. | D. |
已知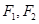 为椭圆
为椭圆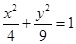 两个焦点,
两个焦点, 为椭圆上一点且
为椭圆上一点且 ,则
,则 ( )
( )
| A.3 | B.9 | C.4 | D.5 |
如果 表示焦点在
表示焦点在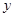 轴上的椭圆,那么实数
轴上的椭圆,那么实数 的取值范围是( )
的取值范围是( )
A.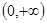 | B.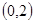 | C.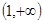 | D.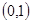 |
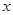 的不等式
的不等式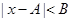 的解集叫
的解集叫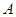 的
的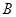 邻域.已知
邻域.已知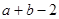 的
的 邻域为区间
邻域为区间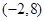 ,其中
,其中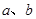 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线 的焦点重合,则椭圆的方程为( . )
的焦点重合,则椭圆的方程为( . )