题目内容
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直, ![]() ,且
,且![]() ,
, ![]() .
.

(1)求二面角![]() 的余弦值;
的余弦值;
(2)已知点![]() 为线段
为线段![]() 上异于
上异于![]() 的点,且
的点,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解得各面法向量,利用向量数量积求向量夹角,最后根据二面角与向量夹角关系求结果(2)设![]() ,根据向量坐标表示距离,再根据距离相等解得
,根据向量坐标表示距离,再根据距离相等解得![]() ,即为
,即为![]() 的值.
的值.
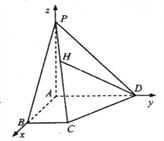
试题解析:以![]() 为正交基底,建立如图所示空间直角坐标系
为正交基底,建立如图所示空间直角坐标系![]() .
.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(1)由题意可知, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则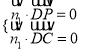 即
即![]() 令
令![]() ,
,
则![]() ,
, ![]() .
.
所以![]() .
.
平面![]() 的法向量为
的法向量为![]() ,
,
所以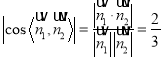 ,
,
所以二面角![]() 的余弦值
的余弦值![]() .
.
(2)由题意可知, ![]() ,
, ![]() ,
,
设![]() ,
,
则![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
化简得![]() ,所以
,所以![]() 或
或![]() .
.
又因为点![]() 异于点
异于点![]() ,所以
,所以![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
【题目】2017年是内蒙古自治区成立70周年.某市旅游文化局为了庆祝内蒙古自治区成立70周年,举办了第十三届成吉思汗旅游文化周.为了了解该市关注“旅游文化周”居民的年龄段分布,随机抽取了![]() 名年龄在
名年龄在![]() 且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.

年龄 |
|
|
|
单人促销价格(单位:元) |
|
|
|
(Ⅰ)根据频率分布直方图,估计该市被抽取市民的年龄的平均数;
(Ⅱ)某旅行社针对“旅游文化周”开展不同年龄段的旅游促销活动,各年龄段的促销价位如表所示.已知该旅行社的运营成本为每人![]() 元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
(Ⅲ)若按照分层抽样的方法从年龄在![]() ,
, ![]() 的居民中抽取
的居民中抽取![]() 人进行旅游知识推广,并在知识推广后再抽取
人进行旅游知识推广,并在知识推广后再抽取![]() 人进行反馈,求进行反馈的居民中至少有
人进行反馈,求进行反馈的居民中至少有![]() 人的年龄在
人的年龄在![]() 的概率.
的概率.
