题目内容
【题目】某同学参加语、数、外三门课程的考试，设该同学语、数、外取得优秀成绩的概率分别为
， 
， 
（
），设该同学三门课程都取得优秀成绩的概率为
，都未取得优秀成绩的概率为
，且不同课程是否取得优秀成绩相互独立.
（1）求
， 
；
（2）设
为该同学取得优秀成绩的课程门数，求
的分布列和数学期望.
【答案】（1）
， 
;（2）见解析.
【解析】试题分析：（1）设该同学语、数、外取得优秀成绩分别为事件
、
、
，可得
，
， 
，由已知条件可知： 
， 
，利用相互独立事件的概率公式列方程组即可得出
， 
的值；（2）由题意可知， 
的可能取值为
，根据独立事件的概率公式以及对立事件的概率公式，可求
各随机变量对应的概率，即可得分布列，利用期望公式可求数学期望的值.
试题解析：（1）设该同学语、数、外取得优秀成绩分别为事件
、
、
∴
， 
， 
，
由已知条件可知： 
， 
∴
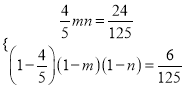又
，则
， 
（2）∵
， 
， 
； 
， 
∴
的分布列为
所以
.
【题目】随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关，某调查小组随机抽取了30名男生、20名女生进行为期一周的跟踪调查，调查结果如下表所示：
平均每天使用手机超过3小时 | 平均每天使用手机不超过3小时 | 合计 | |
男生 | 25 | 5 | 30 |
女生 | 9 | 11 | 20 |
合计 | 34 | 16 | 50 |
(1)能否在犯错误的概率不超过0.01的前提下认为学生使用手机的时间长短与性别有关？
(2)在这20名女生中，调查小组发现共有15人使用国产手机，在这15人中，平均每天使用手机不超过3小时的共有9人.从平均每天使用手机超过3小时的女生中任意选取3人，求这3人中使用非国产手机的人数X的分布列和数学期望.
参考公式： 
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
