Question

【题目】已知函数f（x）=lnx﹣tx+t.

（1）讨论f（x）的单调性；

（2）当t=2时,方程f（x）=m﹣ax恰有两个不相等的实数根x1,x2,证明：.

Answer 1

【答案】（1）当t≤0时,f（x）在（0,+∞）上单调递增；当t＞0时,f（x）在（0,）上单调递增,在（,+∞）上单调递减；（2）证明见解析.

【解析】

(1)求导后分和两种情况讨论极值点的大小关系以及导函数的正负,进而求得原函数的单调区间即可.

(2)代入,根据f（x）=m﹣ax,可得的两根分别为,再消去化简得到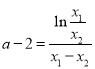,再代入所证的,换元令,进而求导分析导数的正负以及原函数的单调性即可.

（1）f（x）的定义域为（0,+∞）,f′（x）,

当t≤0时,f′（x）＞0恒成立,f（x）在（0,+∞）上单调递增,

当t＞0时,令f′（x）＞0,得0＜x,令f′（x）＜0,得x.

∴f（x）在（0,）上单调递增,在（,+∞）上单调递减.

综上所述,当t≤0时,f（x）在（0,+∞）上单调递增；

当t＞0时,f（x）在（0,）上单调递增,在（,+∞）上单调递减.

（2）证明：由f（x）=m﹣ax,得lnx+（a﹣2）x+2﹣m=0.

令g（x）=lnx+（a﹣2）x+2,则g（x1）=g（x2）=m.

即lnx1+（a﹣2）x1=lnx2+（a﹣2）x2,

∴a﹣2.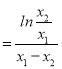

不妨设0＜x1＜x2,要证,

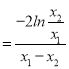只需证2（2﹣a）,即证.

令（c＞1）,g（c）=2lnc﹣c,

∵g′（c）0.

∴g（c）在（1,+∞）上单调递减,则g（c）＜g（1）=0.

故成立.