题目内容
6.已知菱形ABCD的边长为4,∠ABC=$\frac{5π}{6}$,若在菱形内任取一点,则该点到菱形的四个顶点的距离大于1的概率为1-$\frac{π}{8}$.分析 根据几何概型的概率公式求出对应区域的面积进行求解即可.
解答 解:分别以A,B,C,D为圆心,1为半径的圆,
则所以概率对应的面积为阴影部分,
则四个圆在菱形内的扇形夹角之和为2π,
则对应的四个扇形之和的面积为一个整圆的面积S=π×12=π,
∵∠ABC=$\frac{5π}{6}$,
∴∠BAD=$\frac{π}{6}$,
则菱形的面积S=$\frac{1}{2}×4×4×sin\frac{π}{6}×2$=8,
则阴影部分的面积S=8-π,
故所求的概率P=$\frac{8-π}{8}$=1-$\frac{π}{8}$,
故答案为: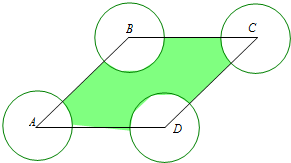 1-$\frac{π}{8}$
1-$\frac{π}{8}$
点评 本题主要考查几何概型的概率的计算,根据对应分别求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
14.下列函数中,既是奇函数,又在定义域内为减函数的是( )
| A. | y=(${\frac{1}{2}}$)x | B. | y=-x2 | C. | y=-x3 | D. | y=log3(-x) |
11. 如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
 如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )
如图是2014年“水仙之春”晚会上,七位评审为某舞蹈打出的分数的茎叶统计图,去掉一个最高分,去掉一个最低分后,所剩数据的平均数和方差分别为( )| A. | 85,1.6 | B. | 84,1.6 | C. | 84,4.84 | D. | 85,4 |