题目内容
17.圆C1:x2+y2+4x+4y+4=0与圆C2:x2+y2-4x-2y-4=0公切线条数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 分别求出两圆的半径和圆心距,由此得到两圆相交,从而能求出两公切线的条数.
解答 解:∵圆C1:x2+y2+4x+4y+4=0的圆心C1(-2,-2),半径r1=2,
圆C2:x2+y2-4x-2y-4=0的圆心C2(2,1),半径r2=3,
|C1C2|=$\sqrt{({2+2)}^{2}+(1+2)^{2}}$=5,
∵|C1C2|=r1+r2,
∴圆C1:x2+y2+4x-4y+4=0与圆C2:x2+y2-4x-10y+13=0相外切,
∴圆C1:x2+y2+4x+4y+4=0与圆C2:x2+y2-4x-2y-4=0公切线条数为3条.
故选:C.
点评 本题考查两圆的公切线的条数的求法,是基础题,解题时要注意两圆位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.4位同学要完成100米的接力跑,要求每个人跑的路程不超过其他任一同学所跑路程的3倍,若某一同学所跑路程为x米,则x的取值范围为( )
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
5.函数f(x)=sinx•ln(x+1)的图象大致为( )
| A. | 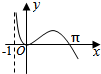 | B. | 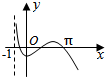 | C. | 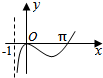 | D. | 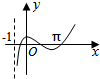 |
12.已知集合A={0,1},B={1,2},则A∪B=( )
| A. | ∅ | B. | {1} | C. | {0,2} | D. | {0,1,2} |
9.过直线x+y+2=0上点P作圆x2+y2=1的两条切线,切点分别为A,B,∠APB=60°,则点P的坐标是( )
| A. | (0,-2)或(-2,0) | B. | (0,2)或(-2,0) | C. | (-2,0) | D. | (0,-2) |