题目内容
16.某校早上7:30开始上课,假设该校学生小张与小王在早上7:00-7:20之间到校,且每人在该时间段的任何时刻到是等可能的,则小张比小王至少早5分钟到校的概率为多少?分析 设小张到校的时间为x,小王到校的时间为y.(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|0≤x≤20,0≤y≤20}是一个矩形区域,则小张比小王至少早5分钟到校事件A={(x,y)|y-x≥5}作出符合题意的图象,由图根据几何概率模型的规则求解即可.
解答 解:设小张到校的时间为x,小王到校的时间为y.
(x,y)可以看成平面中的点试验的全部结果所构成的区域为Ω={(x,y|0≤x≤20,0≤y≤20}是一个矩形区域,对应的面积S=20×20=400,
则小张比小王至少早5分钟到校事件A={x|y-x≥5}作出符合题意的图象,
则符合题意的区域为△ADE,联立$\left\{\begin{array}{l}{y-x=5}\\{y=20}\end{array}\right.$得$\left\{\begin{array}{l}{x=15}\\{y=20}\end{array}\right.$,即D(15,20),
联立$\left\{\begin{array}{l}{y-x=5}\\{x=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=0}\\{y=5}\end{array}\right.$,即E(0,5),
则S△ADE=$\frac{1}{2}$×15×15,
几何概率模型可知小张比小王至少早5分钟到校的概率为$\frac{\frac{1}{2}×15×15}{20×20}$=$\frac{9}{32}$.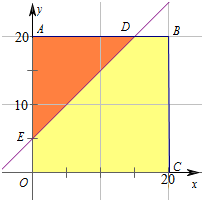
点评 本题考查几何概率模型与模拟方法估计概率,求解的关键是掌握两种求概率的方法的定义及规则,求出对应区域的面积是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.已知向量$\overrightarrow{a}$={1,-1,2},$\overrightarrow{b}$={-2,2,m},且$\overrightarrow{a}$$∥\overrightarrow{b}$,则m的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
11.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “a、b都是有理数”的否定是“a、b都不是有理数” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为真命题 | |
| D. | “x=-1”是“x2-5x-6=0”的必要不充分条件 |
1.方程$\sqrt{{x}^{2}-1}$(x2+y2-4)=0所表示的图形是( )
| A. | 两条直线和一个圆 | B. | 两条直线和两段圆弧 | ||
| C. | 两条线段和两段圆弧 | D. | 四条射线和两段圆弧 |
5.已知函数f(x)=ex-ax有两个零点x1<x2,则下列说法错误的是( )
| A. | a>e | B. | x1+x2>2 | ||
| C. | x1x2>1 | D. | 有极小值点x0,且x1+x2<2x0 |
15.几何体的三视图如图,则其体积为( )


| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | 2π-1 | D. | 4π-1 |