[题目]已知椭圆C的中心在原点.一个焦点F.且长轴长与短轴长的比为.(1)求椭圆C的方程,(2)设点M(m,0)在椭圆C的长轴上.设点P是椭圆上的任意一点.若当最小时.点P恰好落在椭圆的右顶点.求实数m的取值范围. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知椭圆C的中心在原点，一个焦点F(-2,0)，且长轴长与短轴长的比为，

（1）求椭圆C的方程；

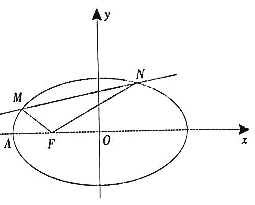
（2）设点M(m,0)在椭圆C的长轴上，设点P是椭圆上的任意一点，若当最小时，点P恰好落在椭圆的右顶点，求实数m的取值范围.

【答案】（1）（2）

【解析】

试题（1）利用待定系数法求椭圆方程;(2)利用点点距公式表示，借助点在曲线上，转化为二次函数的最值问题.

试题解析：

（1）由题意知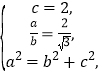解得

所以椭圆方程为

（2）设P(x0,y0),且,

所以|PM|2=(x0-m)2+=-2mx0+m2+12

=-2mx0+m2+12=(x0-4m)2-3m2+12(-4≤x0≤4)

所以|PM|2为关于x0的二次函数,开口向上,对称轴为x0=4m.

由题意知,当x0=4时,|PM|2最小,所以4m≥4,所以m≥1.

又点M(m,0)在椭圆长轴上,所以1≤m≤4

练习册系列答案

相关题目

【题目】在四棱锥中，侧面⊥底面，底面为直角梯形，//，，，，为的中点．

（Ⅰ）求证：PA//平面BEF；

（Ⅱ）若PC与AB所成角为，求的长；

（Ⅲ）在（Ⅱ）的条件下，求二面角F-BE-A的余弦值．

【题目】正方形的四个顶点都在椭圆上，若椭圆的焦点在正方形的内部，则椭圆的离心率的取值范围是（）

A. B. C. D.

【题目】如图，在等腰梯形ABCD中，AB＝2DC＝2，∠DAB＝60°，E为AB的中点．将△ADE与△BEC分别沿ED、EC向上折起，使A、B重合于点P，则三棱锥PDCE的外接球的体积为（）

A. B. C. D.

【题目】如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2＝BD·BC；类似地有命题：在三棱锥A－BCD中，AD⊥平面ABC，若A点在平面BCD内的射影为M，则有S＝S△BCM·S△BCD.上述命题是 (　　)

A. 真命题

B. 增加条件“AB⊥AC”才是真命题

C. 增加条件“M为△BCD的垂心”才是真命题

D. 增加条件“三棱锥A－BCD是正三棱锥”才是真命题

【题目】已知椭圆的离心率为，抛物线的准线被椭圆截得的线段长为．

（1）求椭圆的方程；

（2）如图，点分别是椭圆的左顶点、左焦点直线与椭圆交于不同的两点（都在轴上方）．且．证明：直线过定点，并求出该定点的坐标．

【题目】在△ABC中，角A，B，C的对边分别为a，b，c，若acos2＋ccos2＝b.

(1)求证：a，b，c成等差数列；

(2)若∠B＝60°，b＝4，求△ABC的面积．

【题目】目前我国城市的空气污染越来越严重，空气质量指数一直居高不下，对人体的呼吸系统造成了严重的影响，现调查了某城市500名居民的工作场所和呼吸系统健康，得到列联表如下：

	室外工作	室内工作	合计
有呼吸系统疾病	150
无呼吸系统疾病		100
合计	200

（Ⅰ）请把列联表补充完整；

（Ⅱ）你是否有95%的把握认为感染呼吸系统疾病与工作场所有关；

（Ⅲ）现采用分层抽样从室内工作的居民中抽取一个容量为6的样本，将该样本看成一个总体，从中随机抽取2人，求2人都有呼吸系统疾病的概率.

参考公式与临界表：

	0.100	0.050	0.025	0.010	0.001
	2.706	3.841	5.024	6.635	10.828

【题目】已知数列的前项和为，且，数列满足，且.

（1）求数列，的通项公式；

（2）若，数列的前项和为，若不等式对一切恒成立，求实数的取值范围.

试题分类