题目内容
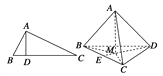
【题目】如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S![]() =S△BCM·S△BCD.上述命题是 ( )
=S△BCM·S△BCD.上述命题是 ( )
A. 真命题
B. 增加条件“AB⊥AC”才是真命题
C. 增加条件“M为△BCD的垂心”才是真命题
D. 增加条件“三棱锥A-BCD是正三棱锥”才是真命题
【答案】A
【解析】因为AD⊥平面ABC,AE平面ABC,BC 平面ABC,
所以AD⊥AE,AD⊥BC.
在△ADE中,AE2=ME·DE,
又A点在平面BCD内的射影为M,
所以AM⊥平面BCD,AM⊥BC,
所以BC⊥平面ADE,
所以BC⊥DE,BC⊥AE.
又![]() ,
,
所以![]() .选A.
.选A.

【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:

①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上台表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
