题目内容
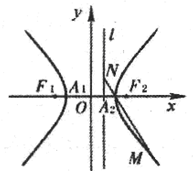
已知两点A(-2,0),B(2,0),直线AM、BM相交于点M,且这两条直线的斜率之积为-
.
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆(x-1)2+y2=r2(0<r<
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.求△OQR的面积的最大值(其中点O为坐标原点).
| 3 |
| 4 |
(Ⅰ)求点M的轨迹方程;
(Ⅱ)记点M的轨迹为曲线C,曲线C上在第一象限的点P的横坐标为1,直线PE、PF与圆(x-1)2+y2=r2(0<r<
| 3 |
| 2 |
(Ⅰ)设点M(x,y),KAMKBM=-
,∴
•
=-
.
整理得点M所在的曲线C的方程:
+
=1(x≠±2).
(Ⅱ)把x=1代入曲线C的方程,可得
+
=1,∵y>0,解得y=
,∴点P(1,
).
∵圆(x-1)2+y2=r2的圆心为(1,0),
∴直线PE与直线PF的斜率互为相反数.
设直线PE的方程为y=k(x-1)+
,
联立
,化为
(4k2+3)x2+(12k-8k2)x+(4k2-12k-3)=0,
由于x=1是方程的一个解,
∴方程的另一解为xQ=
.
同理xR=
.
故直线RQ的斜率为kRQ=
=
=
=
.
把直线RQ的方程y=
x+t代入椭圆方程,消去y整理得x2+tx+t2-3=0.
∴|RQ|=
=
.
原点O到直线RQ的距离为d=
.
∴S△ORQ=
•
•
•
=
≤
•
=
.当且仅当t=±
时取等号.
∴△OQR的面积的最大值为
.
| 3 |
| 4 |
| y |
| x+2 |
| y |
| x-2 |
| 3 |
| 4 |
整理得点M所在的曲线C的方程:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)把x=1代入曲线C的方程,可得
| 1 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |

∵圆(x-1)2+y2=r2的圆心为(1,0),
∴直线PE与直线PF的斜率互为相反数.
设直线PE的方程为y=k(x-1)+
| 3 |
| 2 |
联立
|
(4k2+3)x2+(12k-8k2)x+(4k2-12k-3)=0,
由于x=1是方程的一个解,
∴方程的另一解为xQ=
| 4k2-12k-3 |
| 4k2+3 |
同理xR=
| 4k2+12k-3 |
| 4k2+3 |
故直线RQ的斜率为kRQ=
| yR-yQ |
| xR-xQ |
-k(xR-1)+
| ||||
| xR-xQ |
-k(
| ||
|
| 1 |
| 2 |
把直线RQ的方程y=
| 1 |
| 2 |
∴|RQ|=
[1+(
|
| ||
| 2 |
| 4-t2 |
原点O到直线RQ的距离为d=
| |2t| | ||
|
∴S△ORQ=
| 1 |
| 2 |
| ||
| 2 |
| 4-t2 |
| |2t| | ||
|
| ||
| 2 |
| t2(4-t2) |
| ||
| 2 |
| t2+(4-t2) |
| 2 |
| 3 |
| 2 |
∴△OQR的面积的最大值为
| 3 |

练习册系列答案
相关题目
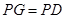 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.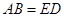 .
.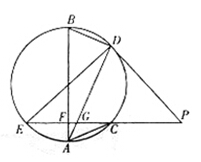


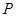 作圆的切线
作圆的切线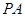 (
(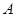 为切点),再作割线
为切点),再作割线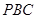 分别交圆于
分别交圆于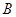 、
、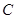 , 若
, 若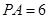 ,
, 是圆
是圆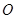 的切线,切点为
的切线,切点为 ,
, 交圆
交圆 、
、 两点,且
两点,且 ,
,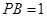 ,则
,则 的长为 .
的长为 .