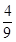题目内容
已知圆C1:x2+y2=
,直线l:y=x+m(m>0)与圆C1相切,且交椭圆C2:
+
=1(a>b>0)于A1,B1两点,c是椭圆C2的半焦距,c=
b.
(1)求m的值;
(2)O为坐标原点,若
⊥
,求椭圆C2的方程;
(3)在(2)的条件下,设椭圆C2的左、右顶点分别为A,B,动点S(x1,y1)∈C2(y1>0)直线AS,BS与直线x=
分别交于M,N两点,求线段MN的长度的最小值.
| 4 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求m的值;
(2)O为坐标原点,若
| OA1 |
| OB1 |
(3)在(2)的条件下,设椭圆C2的左、右顶点分别为A,B,动点S(x1,y1)∈C2(y1>0)直线AS,BS与直线x=
| 34 |
| 15 |
(1)∵直线l:y=x+m(m>0)与圆C1相切,
∴
=
,∴m=
;
(2)直线l:y=x+
代入椭圆C2:
+
=1(a>b>0),可得:
(b2+a2)x2+
a2x+
a2-a2b2=0
设A1(x1,y1),B1(x2,y2),则:
x1+x2=-
,x1x2=
,y1y2=
,
∵
⊥
,
∴x1x2+y1y2=
+
=0,
∴4(b2+a2)-5a2b2=0,
∵c=
b,
∴a2=4b2,
∴a=2,b=1,
∴椭圆C的方程为
+y2=1;
(3 ) 易知椭圆C的左,右顶点坐标为A(-2,0),B(2,0),直线AS的斜率k显然存在,且k>0,
故可设直线AS的方程为y=k(x+2),从而M(
,
)
由
,得(1+4k2)x2+16k2x+16k2-4=0
设S(x0,y0),则(-2)x0=
,得x0=
,
从而y0=
,即S(
,
).
又B(2,0),故直线BS的方程为y=-
(x-2),
x=
时,y=-
,
∴N(
,-
),
又k>0,∴|MN|=
+
≥2
=
,
当且仅当
=
时,即k=
时等号成立,
∴k=
时,线段MN的长度取最小值
.
∴
| |m| | ||
|
|
2
| ||
| 5 |
(2)直线l:y=x+
2
| ||
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
(b2+a2)x2+
4
| ||
| 5 |
| 8 |
| 5 |
设A1(x1,y1),B1(x2,y2),则:
x1+x2=-
4
| ||
| 5(b2+a2) |
| 8a2-5a2b2 |
| 5(b2+a2) |
| 40b2+25a2b2 |
| 25(a2+b2) |
∵
| OA1 |
| OB1 |
∴x1x2+y1y2=
| 8a2-5a2b2 |
| 5(b2+a2) |
| 40b2+25a2b2 |
| 25(a2+b2) |
∴4(b2+a2)-5a2b2=0,
∵c=
| 3 |
∴a2=4b2,
∴a=2,b=1,
∴椭圆C的方程为
| x2 |
| 4 |
(3 ) 易知椭圆C的左,右顶点坐标为A(-2,0),B(2,0),直线AS的斜率k显然存在,且k>0,
故可设直线AS的方程为y=k(x+2),从而M(
| 34 |
| 15 |
| 64k |
| 15 |
由
|
设S(x0,y0),则(-2)x0=
| 16k2-4 |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
从而y0=
| 4k |
| 1+4k2 |
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
又B(2,0),故直线BS的方程为y=-
| 1 |
| 4k |
x=
| 34 |
| 15 |
| 1 |
| 15k |
∴N(
| 34 |
| 15 |
| 1 |
| 15k |
又k>0,∴|MN|=
| 64k |
| 15 |
| 1 |
| 15k |
|
| 16 |
| 15 |
当且仅当
| 64k |
| 15 |
| 1 |
| 15k |
| 1 |
| 8 |
∴k=
| 1 |
| 8 |
| 16 |
| 15 |

练习册系列答案
相关题目
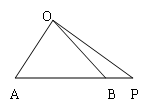
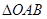 是等腰三角形,
是等腰三角形,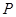 是底边
是底边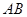 延长线上一点,
延长线上一点,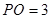 ,
,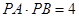 ,则腰长
,则腰长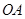 = .
= .
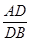 =2,那么△ADE与四边形DBCE的面积比是( )
=2,那么△ADE与四边形DBCE的面积比是( )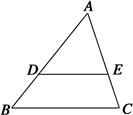
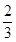 B.
B.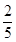 C.
C.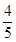 D.
D.