题目内容
已知抛物线Σ1:y=
x2的焦点F在椭圆Σ2:
+
=1(a>b>0)上,直线l与抛物线Σ1相切于点P(2,1),并经过椭圆Σ2的焦点F2.
(1)求椭圆Σ2的方程;
(2)设椭圆Σ2的另一个焦点为F1,试判断直线FF1与l的位置关系.若相交,求出交点坐标;若平行,求两直线之间的距离.
| 1 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆Σ2的方程;
(2)设椭圆Σ2的另一个焦点为F1,试判断直线FF1与l的位置关系.若相交,求出交点坐标;若平行,求两直线之间的距离.
(1)抛物线y=
x2即x2=4y的焦点F(0,1),
由题意可得
+
=1,解得b=1,
切线l的斜率k=y/=
x|x=2=1,
∴切线l方程为y-1=x-2,即x-y-1=0,
令y=0,解得x=1.∴焦点F2(1,0),即c=1.
∴a=
=
,
椭圆Σ2的方程为
+y2=1.
(2)由(1)得F1(-1,0),
直线FF1的方程为
=
,即x-y+1=0,
∵kFF1=k=1,且F1(-1,0)不在直线l上,
∴直线FF1∥l,
FF1与l之间的距离即为F(0,1)到直线l的距离d=
=
.
| 1 |
| 4 |
由题意可得
| 0 |
| a2 |
| 1 |
| b2 |
切线l的斜率k=y/=
| 1 |
| 2 |
∴切线l方程为y-1=x-2,即x-y-1=0,
令y=0,解得x=1.∴焦点F2(1,0),即c=1.
∴a=
| b2+c2 |
| 2 |
椭圆Σ2的方程为
| x2 |
| 2 |
(2)由(1)得F1(-1,0),
直线FF1的方程为
| y-0 |
| 1-0 |
| x-(-1) |
| 0-(-1) |
∵kFF1=k=1,且F1(-1,0)不在直线l上,
∴直线FF1∥l,
FF1与l之间的距离即为F(0,1)到直线l的距离d=
| |0-1-1| | ||
|
| 2 |

练习册系列答案
相关题目
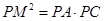 ;
;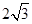 ,OA=
,OA=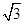 OM,求MN的长.
OM,求MN的长.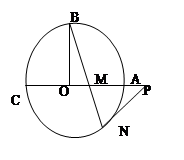
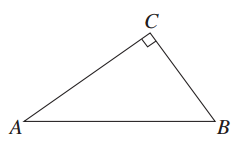
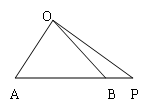
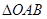 是等腰三角形,
是等腰三角形,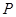 是底边
是底边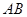 延长线上一点,
延长线上一点,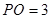 ,
,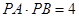 ,则腰长
,则腰长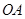 = .
= .
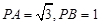 ,则
,则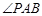 =_________.
=_________.