题目内容
已知椭圆C:
+
=1(a>b>0)的离心率e=
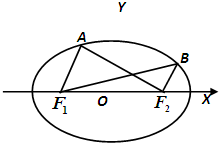
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
.
(1)求椭圆C的方程;
(2)过原点且斜率为
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
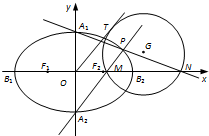
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
2
| ||
| 5 |
(1)求椭圆C的方程;
(2)过原点且斜率为
| 1 |
| 2 |
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.

(1)因为椭圆C的离心率e=
,
故设a=2m,c=
m,则b=m.
直线A2B2方程为bx-ay-ab=0,
即mx-2my-2m2=0.
所以
=
,解得m=1.
所以a=2,b=1,椭圆方程为
+y2=1.
(2)由
+y2=1及y=
x得:
x=±
,则E(
,
),F(-
,-
),
又∵椭圆
+y2=1的右焦点F2的坐标为(
,0)
∴
=(
-
,
),
=(-
-
,-
),
∴
•
=(
-
)×(-
-
)+
×(-
)=
>0,
∴∠EF2F是锐角
(3)由(1)可知A1(0,1)A2(0,-1),设P(x0,y0),
直线PA1:y-1=
x,令y=0,得xN=
;
直线PA2:y+1=
x,令y=0,得xM=
;
解法一:设圆G的圆心为(
(
-
),h),
则r2=[
(
-
)-
]2+h2=
(
+
)2+h2.
OG2=
(
-
)2+h2.
OT2=OG2-r2=
(
-
)2+h2-
(
+
)2-h2=
.
而
+y02=1,所以x02=4(1-y02),所以OT2=4,
所以OT=2,即线段OT的长度为定值2.…(16分)
解法二:OM•ON=|(-
)•
|=
,
而
+y02=1,所以x02=4(1-y02),所以OM•ON=4.
由切割线定理得OT2=OM•ON=4.
所以OT=2,即线段OT的长度为定值2.…(16分)
| ||
| 2 |
故设a=2m,c=
| 3 |
直线A2B2方程为bx-ay-ab=0,
即mx-2my-2m2=0.
所以
| 2m2 | ||
|
2
| ||
| 5 |
所以a=2,b=1,椭圆方程为
| x2 |
| 4 |
(2)由
| x2 |
| 4 |
| 1 |
| 2 |
x=±
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
又∵椭圆
| x2 |
| 4 |
| 3 |
∴
| F2E |
| 2 |
| 3 |
| ||
| 2 |
| F2F |
| 2 |
| 3 |
| ||
| 2 |
∴
| F2E |
| F2F |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴∠EF2F是锐角
(3)由(1)可知A1(0,1)A2(0,-1),设P(x0,y0),
直线PA1:y-1=
| y0-1 |
| x0 |
| x0 |
| y0-1 |
直线PA2:y+1=
| y0+1 |
| x0 |
| x0 |
| y0+1 |
解法一:设圆G的圆心为(
| 1 |
| 2 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
则r2=[
| 1 |
| 2 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
| x0 |
| y0+1 |
| 1 |
| 4 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
OG2=
| 1 |
| 4 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
OT2=OG2-r2=
| 1 |
| 4 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
| 1 |
| 4 |
| x0 |
| y0+1 |
| x0 |
| y0-1 |
| ||
1-
|
而
| ||
| 4 |
所以OT=2,即线段OT的长度为定值2.…(16分)
解法二:OM•ON=|(-
| x0 |
| y0-1 |
| x0 |
| y0+1 |
| ||
1-
|
而
| ||
| 4 |
由切割线定理得OT2=OM•ON=4.
所以OT=2,即线段OT的长度为定值2.…(16分)

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目